Penetration & Shielding
- Page ID
- 1704
Penetration and shielding are two underlying principles in determining the physical and chemical properties of elements. We can predict basic properties of elements by using shielding and penetration characteristics to assess basic trends.
Introduction
Electrons are negatively charged and are pulled pretty close to each other by their attraction to the positive charge of a nucleus. The electrons are attracted to the nucleus at the same time as electrons repel each other. The balance between attractive and repulsive forces results in shielding. The orbital (n) and subshell (ml) define how close an electron can approach the nucleus. The ability of an electron to get close to the nucleus is penetration.
Coulomb's Law (an analogy with classical physics) can be used to describe the attraction and repulsion between atomic particles:
\[ F=k \dfrac{q_1q_1}{r^2} \label{1}\]
The force that an electron feels is dependent on the distance from the nearest charge (i.e., an electron, usually with bigger atoms and on the outer shells) and the amount of charge. More distance between the charges will result in less force, and more charge will have more force of attraction or repulsion.
In the simplest case, every electron in an atom would feel the same amount of "pull" from the nucleus. For example, in Li, all three electrons might "feel" the +3 charge from the nucleus. However, this is not the case when observing atomic behavior. When considering the core electrons (or the electrons closest to the nucleus), the nuclear charge "felt" by the electrons (Effective Nuclear Charge (\(Z_{eff}\))) is close to the actual nuclear charge. As you proceed from the core electrons to the outer valence electrons, \(Z_{eff}\) falls significantly. This is because of shielding, or simply the electrons closest to the nucleus decrease the amount of nuclear charge affecting the outer electrons. Shielding is caused by the combination of partial neutralization of nuclear charge by core electrons, and by electron-electron repulsion.
The amount of charge felt by an electron depends on its distance from the nucleus. The closer an electron comes to the nucleus, or the more it penetrates, the stronger its attraction to the nucleus. Core electrons penetrate more and feel more of the nucleus than the other electrons.
\[ F_{electron-nucleus}=k \dfrac{Ze^2}{r^2} \label{2}\]
with
- \(Z\) is the charge of the nucleus (i.e., number of protons)
- \(e\) is the charge of an electron or proton
- r is the radius, or distance between the proton and the electron
Penetration and shielding result in an Effective force (\(F_{eff}\)) that holds the outer electrons to the atom, akin to Equation \(\ref{2}\), but with \(Z_{eff}\) substituted for \(Z\):
\[ F_{eff}=k \dfrac{Z_{eff}e^2}{r^2} \label{3}\]
Orbital Penetration
Penetration describes the proximity to which an electron can approach to the nucleus. In a multi-electron system, electron penetration is defined by an electron's relative electron density (probability density) near the nucleus of an atom. Electrons in different orbitals have different wavefunctions and therefore different radial distributions and probabilities (defined by quantum numbers n and ml around the nucleus). In other words, penetration depends on the shell (n) and subshell (ml). For example, we see that since a 2s electron has more electron density near the nucleus than a 2p electron, it is penetrating the nucleus of the atom more than the 2p electron. The penetration power of an electron, in a multi-electron atom, is dependent on the values of both the shell and subshell.
Within the same shell value (n), the penetrating power of an electron follows this trend in subshells (ml):
s>p>d>f
And for different values of shell (n) and subshell (l), penetrating power of an electron follows this trend:
1s>2s>2p>3s>3p>4s>3d>4p>5s>4d>5p>6s>4f....
and the energy of an electron for each shell and subshell goes as follows...
1s<2s<2p<3s<3p<4s<3d<4p....
The electron probability density for s-orbitals is highest in the center of the orbital, or at the nucleus. If we imagine a dartboard that represents the circular shape of the s-orbital and if the darts landed in correlation to the probability to where and electron would be found, the greatest dart density would be at the 50 points region but most of the darts would be at the 30 point region. When considering the 1s-orbital, the spherical shell of 53 pm is represented by the 30 point ring.
Electrons which experience greater penetration experience stronger attraction to the nucleus, less shielding, and therefore experience a larger Effective Nuclear Charge (\(Z_{eff}\)), but shield other electrons more effectively.
Shielding
An atom (assuming its atomic number is greater than 2) has core electrons that are extremely attracted to the nucleus in the middle of the atom. However the number of protons in the nucleus are never equal to the number of core electrons (relatively) adjacent to the nucleus. The number of protons increase by one across the periodic table, but the number of core electrons change by periods. The first period has no core electrons, the second has 2, the third has 10, and etc. This number is not equal to the number of protons. So that means that the core electrons feel a stronger pull towards the nucleus than any other electron within the system. The valence electrons are farther out from the nucleus, so they experience a smaller force of attraction.
Shielding refers to the core electrons repelling the outer rings and thus lowering the 1:1 ratio. Hence, the nucleus has "less grip" on the outer electrons and are shielded from them. Electrons that have greater penetration can get closer to the nucleus and effectively block out the charge from electrons that have less proximity. For example, \(Z_{eff}\) is calculated by subtracting the magnitude of shielding from the total nuclear charge. The value of \(Z_{eff}\) will provide information on how much of a charge an electron actually experiences.

Because the order of electron penetration from greatest to least is s, p, d, f; the order of the amount of shielding done is also in the order s, p, d, f.
Since the 2s electron has more density near the nucleus of an atom than a 2p electron, it is said to shield the 2p electron from the full effective charge of the nucleus. Therefore the 2p electron feels a lesser effect of the positively charged nucleus of the atom due to the shielding ability of the electrons closer to the nucleus than itself, (i.e. 2s electron).
These electrons that are shielded from the full charge of the nucleus are said to experience an effective nuclear charge (\(Z_{eff}\))of the nucleus, which is some degree less than the full nuclear charge an electron would feel in a hydrogen atom or hydrogenlike ions. The effective nuclear charge of an atom is given by the equation:
\[ Z_{eff}=Z-S \label{4}\]
where.
- \(Z\) is the atomic number (number of protons in nucleus) and
- \(S\) is the shielding constant
We can see from this equation that the effective nuclear charge of an atom increases as the number of protons in an atom increases. Therefore as we go from left to right on the periodic table the effective nuclear charge of an atom increases in strength and holds the outer electrons closer and tighter to the nucleus. This phenomena can explain the decrease in atomic radii we see as we go across the periodic table as electrons are held closer to the nucleus due to increase in number of protons and increase in effective nuclear charge.
What is the effective attraction \(Z_{eff}\) experienced by the valence electrons in the three isoelectronic species: the fluorine anion, the neutral neon atom, and sodium cation?
Solution
Each species has 10 electrons, and the number of nonvalence electrons is 2 (10 total electrons - 8 valence) but the effective nuclear charge varies because each has a different atomic number \(A\).
The charge \(Z\) of the nucleus of a fluorine atom is 9, but the valence electrons are screened appreciably by the core electrons (four electrons from the 1s and 2s orbitals) and partially by the 7 electrons in the 2p orbitals.
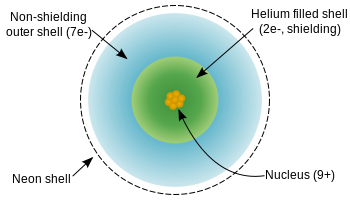
Diagram of a fluorine atom showing the extent of effective nuclear charge. (CC BY-SA- 3.0; Wikipedia).
- \(Z_\mathrm{eff}(\mathrm{F}^-) = 9 - 2 = 7+\)
- \(Z_\mathrm{eff}(\mathrm{Ne}) = 10 - 2 = 8+\)
- \(Z_\mathrm{eff}(\mathrm{Na}^+) = 11 - 2 = 9+\)
So the sodium cation has the greatest effective nuclear charge, and thus the smallest radius.
Radial Distribution Graphs
A radial distribution function graph describes the distribution of orbitals with the effects of shielding (Figure \(\PageIndex{2}\)). The small peak of the 2s orbital shows that the electrons in the 2s orbital are closest to the nucleus. Therefore, it is the electrons in the 2p orbital of Be that are being shielded from the nucleus, by the electrons in the 2s orbital.
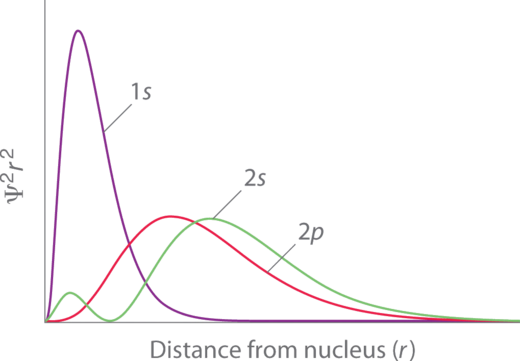
The following is the radial distribution of the 1s and 2s orbitals. Notice the 1s orbital is shifted to the right, while the 2s orbital has a node.
Periodic Trends Due to Penetration and Shielding
- Effective Nuclear Charge (\(Z_{eff}\)): The effective nuclear charge increases from left to right and increases from top to bottom on the periodic table.
- Atomic Radius: The atomic radius decreases from left to right, and increases from top to bottom.
- Ionization Energies: The ionization energies increase from left to right, and decrease from top to bottom.
- Electronegativity: The electronegativity of the elements is highest near flourine. In general, it increases from left to right and decreases from top to bottom.
Questions
- Which orbital is more effective in shielding? 1s or 2p?
- True/False: The greater the penetration of an orbital, the greater the shielding capability of that orbital.
- Find the \(Z_{eff}\)of
- Mg
- C
- F
- Ca
- Which of these have the smallest electron affinity? B, C, N, O, or F.
- Which atom has a stronger effective nuclear charge and why? (assuming S is the same in both cases) Li, or N
- Why does the Hydrogen electron experiences the full charge of the nucleus without any shielding?
- Which atom has a smaller radii? Be or F?
- Which electron has higher energy level? 2s or 2p? and why?
- Why do the orbitals of a hydrogen atom increase energy as follows: 1s<2s=2p<3s=3p=3d<4s=4p=4d<....
- Which electrons shields better in an atom? 2s or 2p? 3p or 3d?
- Why can we relate classical physics to quantum mechanics when it comes to subatomic activity?
- What is penetration?
Solutions
- 1s
- T
-
- a. 12-2 =10
- b. 6-4=2
- c. 9-7=2
- d. 20-2=18
- -
- nitrogen atom has a stronger effective nuclear charge than lithium due to its greater number of protons in the nucleus holding the electrons tighter.
- Hydrogen atom has only one electron total, therefore there are no other, lower energy (more penetrating), electrons available to help shield this electron from the nucleus.
- Fluorine has a smaller radii than Beryllium due to its greater number of protons providing a greater effective nuclear charge on the outer electrons and therefore pulling them in tighter and providing a smaller atomic radii.
- 2p has higher energy level because the negatively charged electron experiences less of an effective nuclear charge than the 2s electron.
- because a Hydrogen atom has only one electron, that experiences no shielding from other electrons and therefore its energy level only depends on its distance away from the nucleus, which is dependent on it value of (n).
- 2s shields the atom better than 2p because the s orbitals is much closer and surrounds the nucleus more than the p orbitals, which extend farther out. 3p shields better than 3d, because p orbitals are closer to the nucleus than the 3d orbitals.
- Classical physics and quantum mechanics both can deal with subatomic activity such as electron interactions, orbital location, size, and shape, and distances to find forces of attractions.
- Penetration is how well the outer electrons are shielded from the nucleus by the core electrons. The outer electrons therefore experience less of an attraction to the nucleus.
References
- Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, and Jeffry D. Madura. General Chemistry: Principles and Modern Applications, Ninth Edition. Pearson Education Inc. Upper Saddle River, New Jersey: 2007.
- Raymond Chang. Physical Chemistry for Biological Sciences. Sausalito, California: University Science Books, 2005
- R. S. Mulliken, Electronic Structures of Molecules and Valence. II General Considerations, Physical Review, vol. 41, pp. 49-71 (1932)
- Anastopoulos, Charis (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 236–237. ISBN 0691135126. http://books.google.com/?id=rDEvQZhpltEC&pg=PA236.
Contributors and Attributions
- Sidra Ayub (UCD), Alan Chu (UCD)

