Membrane Potentials
- Page ID
- 257
Membrane potential is what we use to describe the difference in voltage (or electrical potential) between the inside and outside of a cell.
Introduction
Without membrane potentials human life would not be possible. All living cells maintain a potential difference across their membrane. Simply stated, membrane potential is due to disparities in concentration and permeability of important ions across a membrane. Because of the unequal concentrations of ions across a membrane, the membrane has an electrical charge. Changes in membrane potential elicit action potentials and give cells the ability to send messages around the body. More specifically, the action potentials are electrical signals; these signals carry efferent messages to the central nervous system for processing and afferent messages away from the brain to elicit a specific reaction or movement. Numerous active transports embedded within the cellular membrane contribute to the creation of membrane potentials, as well as the universal cellular structure of the lipid bilayer. The chemistry involved in membrane potentials reaches to many scientific disciplines. Chemically it involves molarity, concentration, electrochemistry and the Nernst equation. From a physiological standpoint, membrane potential is responsible for sending messages to and from the central nervous system. It is also very important in cellular biology and shows how cell biology is fundamentally connected with electrochemistry and physiology. The bottom line is that membrane potentials are at work in your body right now and always will be as long as you live.
History
The subject of membrane potential stretches across multiple scientific disciplines; Membrane Potential plays a role in the studies of Chemistry, Physiology and Biology. The culmination of the study of membrane potential came in the 19th and early 20th centuries. Early in the 20th century, a man named professor Bernstein hypothesized that there were three contributing factors to membrane potential; the permeability of the membrane and the fact that [K+] was higher inside and lower on the outside of the cell. He was very close to being correct, but his proposal had some flaws. Walther H. Nernst, notable for the development of the Nernst equation and winner of 1920 Nobel Prize in chemistry, was a major contributor to the study of membrane potential. He developed the Nernst equation to solve for the equilibrium potential for a specific ion. Goldman, Hodgkin and Katz furthered the study of membrane potential by developing the Goldman-Hodgkin-Katz equation to account for any ion that might permeate the membrane and affect its potential. The study of membrane potential utilizes electrochemistry and physiology to formulate a conclusive idea of how charges are separated across a membrane.
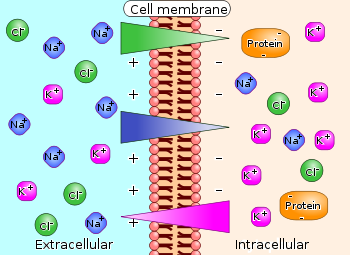
Figure 1. Differences in concentration of ions on opposite sides of a cellular membrane produce a voltage difference called the membrane potential. The largest contributions usually come from sodium (Na+) and chloride (Cl–) ions which have high concentrations in the extracellular region, and potassium (K+) ions, which along with large protein anions have high concentrations in the intracellular region. Calcium ions, which sometimes play an important role, are not shown.
Membrane Potential and Cellular Biology
In discussing the concept of membrane potentials and how they function, the creation of a membrane potential is essential. The lipid bilayer structure of the cellular membrane, with its lipid-phosphorous head and fatty acid tail, provides a perfect building material that creates both a hydrophobic and hydrophilic side to the cellular membrane. The membrane is often referred to as a mosaic model because of its semi-permeability and its ability to keep certain substances from entering the cell. Molecules such as water can diffuse through the cell based on concentration gradients; however, larger molecules such as glucose or nucleotides require channels. The lipid bilayer also houses the Na+/K+ pump, ATPase pump, ion transporters, and voltage gated channels, and it is the site of vesicular transport. The structure regulates which ions enter and exit to determine the concentration of specific ions inside of the cell.
Why is membrane potential essential to the survival of all living creatures?
Animals and plants require the breakdown of organic substances through cellular respiration to generate energy. This process, which produces ATP, is dependent on the electron transport chain. Electrons travel down this path to be accepted by oxygen or other electron acceptors. The initial electrons are obtained from the breakdown of water molecules. The hydrogen build up in the extracellular fluid leaving a gradient. As per membrane potentials, when there a gradient, the molecules flow in the opposite direction. In this case, hydrogen flows back into the cell through a protein known as ATP synthase which creates ATP in the process. This action is essential to life because the number of ATP created from each glucose increases drastically. Chemical disequilibrium and membrane potentials allow bodily functions to take place.
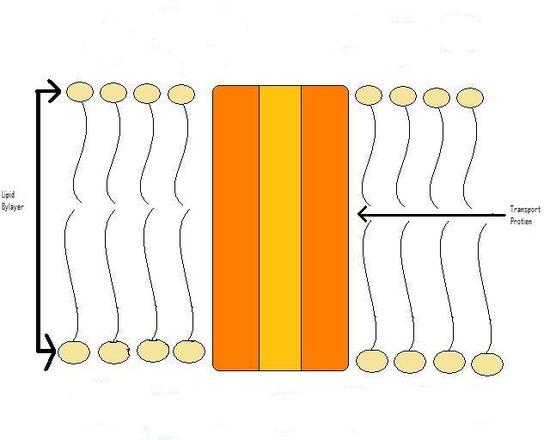
Figure 2
Transport proteins, more specifically the 'active' transport proteins, can pump ions and molecules against their concentration gradient. This is the main source of charge difference across the cellular membrane.
Physiology of Membrane Potential
Understanding Membrane Potential
The following points should help you to understand how membrane potential works
- The difference between the electrical and chemical gradient is important.
- Electrical Gradient
- Opposes the chemical gradient.
- Represents the difference in electrical charge across the membrane
- Chemical Gradient
- Opposes the electrical gradient
- Represents the difference in the concentration of a specific ion across the membrane.
- A good example is K+. The membrane is very permeable to K+ and the [K+] inside the cell is great, therefore a positive charge is flowing out of the cell along with K+. The [K+] inside the cell decreases causing the concentration gradient to flow towards the outside of the cell. This also causes the inside of the cell to become more electronegative increasing its electrical gradient.
- Electrical Gradient
- The Nernst equation can help us relate the numerical values of concentration to the electrical gradient.
- Leak Channels
- Channels that are always open
- Permit unregulated flow of ions down an electrochemical gradient.
- Na+/K+ ATPase Pump
- Actively transports Na+ out of the cell and K+ into the cell.
- Helps to maintain the concentration gradient and to counteract the leak channels.
Membrane Potential and Physiology of Human Nerve Cells
Human nerve cells work mainly on the concept of membrane potentials. They transmit chemicals known as serotonin or dopamine through gradients. The brain receives these neurotransmitters and uses it to perform functions.
- Na+ has a much higher concentration outside of the cell and the cell membrane is very impermeable to Na+
- K+ has a high concentration inside the cell due to the fact that the cell membrane is very permeable to K+
- A- is used to refer to large ions that are found completely inside of the cell and cannot penetrate the cell membrane.
Concentration (in Millimoles/ Liter) and permeability of Ions Responsible for Membrane Potential in a Resting Nerve Cell
| ION | Extracellular | Intracellular | Relative Permeability |
|---|---|---|---|
| Na+ | 150 | 15 | 1 |
| K+ | 5 | 150 | 25-30 |
| A- | 0 | 65 | 0 |
Check out this YouTube video if you want to know more about how the Na+/K+ pump and how the membrane potential works. www.youtube.com/watch?v=iA-Gdkje6pg
How To Calculate A Membrane Potential
The calculation for the charge of an ion across a membrane, The Nernst Potential, is relatively easy to calculate. The equation is as follows: (RT/zF) log([X]out/[X]in). RT/F is approximately 61, therefore the equation can be written as
(61/z) ln([X]out/[X]in)
- R is the universal gas constant (8.314 J.K-1.mol-1).
- T is the temperature in Kelvin (°K = °C + 273.15).
- z is the ionic charge for an ion. For example, z is +1 for K+, +2 for Mg2+, -1 for F-, -1 for Cl-, etc. Remember, z does not have a unit.
- F is the Faraday's constant (96485 C.mol-1).
- [X]out is the concentration of the ion outside of the species. For example the molarity outside of a neuron.
- [X]in is the concentration of the ion inside of the species. For example, the molarity inside of a neuron.
The only difference in the Goldman-Hodgkin-Katz equation is that is adds together the concentrations of all permeable ions as follows
(RT/zF) log([K+]o+[Na+]o+[Cl-]o /[K+]i+[Na+]i+[Cl-]i)
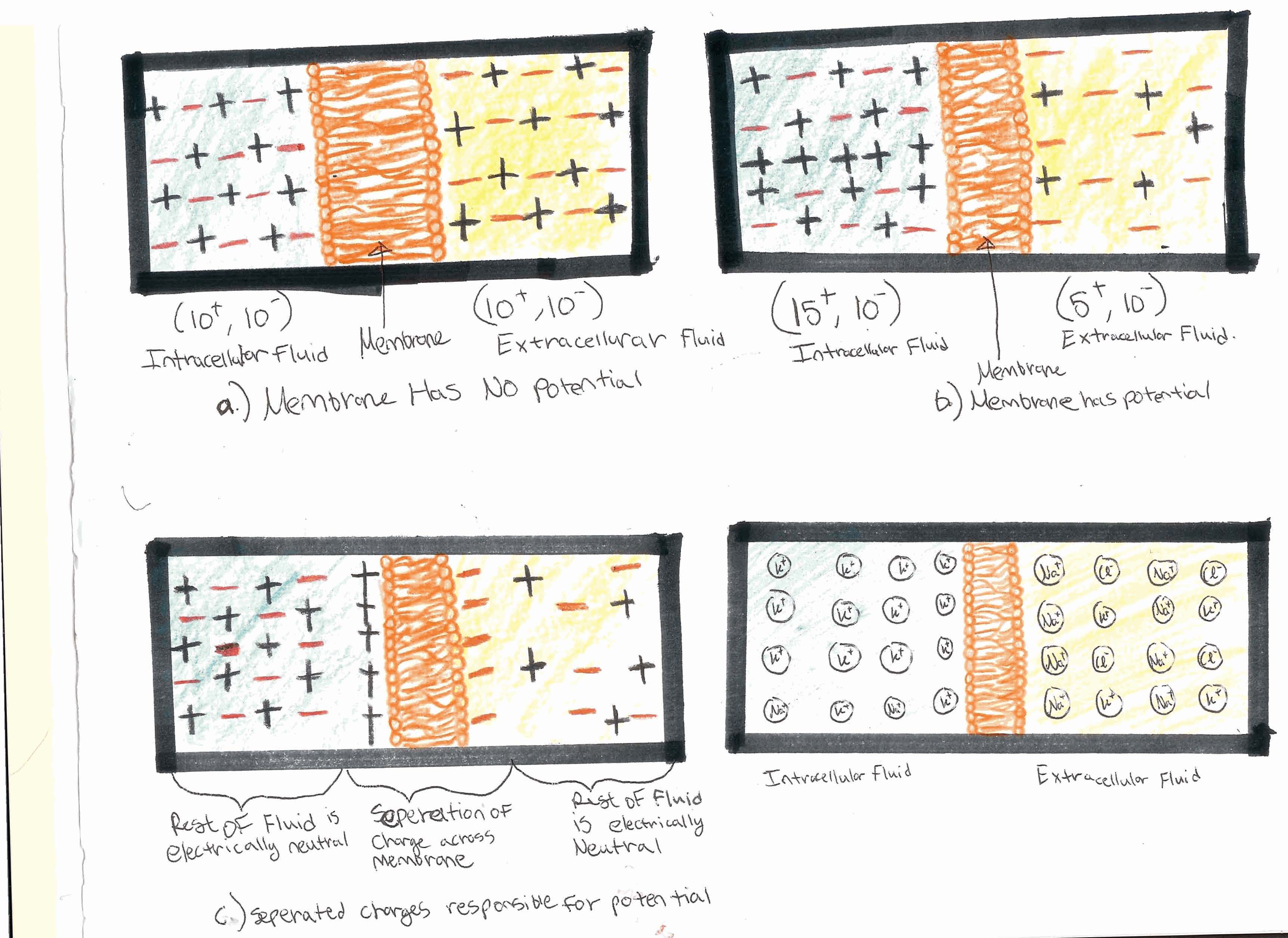
Figure 3. (Clockwise From Upper Left) 1) The charges are equal on both sides; therefore the membrane has no potential. 2)There is an unbalance of charges, giving the membrane a potential. 3) The charges line up on opposite sides of the membrane to give the membrane its potential. 4) A hypothetical neuron in the human body; a large concentration of potassium on the inside and sodium on the outside.
References
- Kaiser, Chris A., et al. Molecular Cell Biology. 6th ed. New York. W. H. Freeman, 2007.
- Orians, Gordon H., et al. Life: The Science of Biology. 8th ed. Gordonville, VA. Sinaver Associates, Inc., 2008.,
- Petrucci, Ralph H., et al. General Chemistry: Principles and Modern Applications. 9th ed. New Jersey. Pearson Education International, 2007.Fuel Cells#
- Sherwood, Lauralee. Human Physiology: From Cells to Systems (International Edition). International ed ed. New York: Brooks Cole, 2009. Print.
- Hietler, W.J.. "Membrane Potential Tutorial." St. Andrews Biology Dept.. St. Andrews University., 13 Aug. 2007. Web. 24 May 2010. <http:/http://www.st-andrews.ac.uk/~wjh/neurotut/
Problems
1. List the following in order from highest to lowest permeability. A-, K+, Na+
2. Which of the following statement is NOT true?
- The membrane potential usually requires a minimal difference of electrocharges across the membrane
- Membrane impermeability plays a role in membrane potentials.
- Membrane potential exists in all cellular structures, except for neurons.
- The active transports play a vital role in membrane potentials.
3. What would be the equilibrium potential for the ion K+ be if [K+]in= 5mM and [K+]in=150mM?
4. True or false: At resting membrane potential, the inside of the membrane is slightly negatively charged while the outside is slightly positively charged.
Answers:
1. K+ > Na+ > A-
2. Answer c.)is not true; membrane potential exists in neurons and is responsible for action potential propagation in neurons.
3. Ek+ = (61/z) log([K+]out/[K+]in) = (61/1) log([5mM]/[150mM]) = -90mV
z=1
4. True. The resting membrane potential is negative as a result of this disparity in concentration of charges.
Contributors
- Dan Chong, Matt Klingler (UCD)

