6. Acid-Base Indicators
- Page ID
- 3856
This page describes how simple acid-base indicators work, and how to choose the right one for a particular titration.
Indicators as weak acids
Litmus
Litmus is a weak acid and is one of the oldest forms of a pH indicator and is used to test materials for acidity.
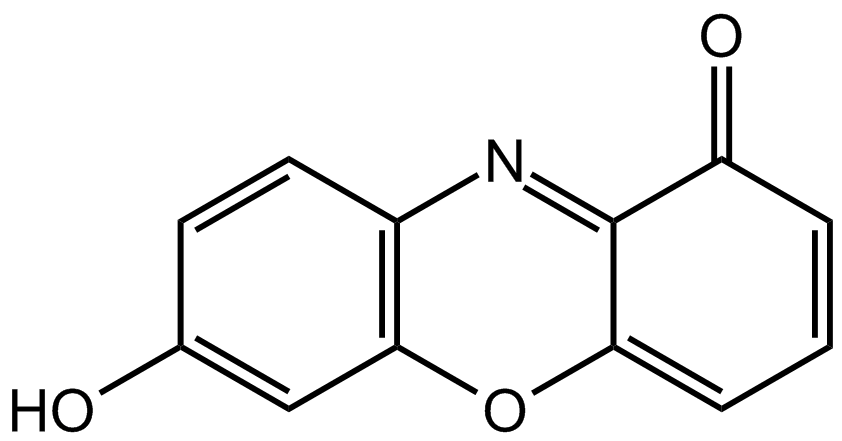
Chemical structure of 7-hydroxyphenoxazone, the chromophore of litmus components.
It has a seriously complicated molecule which we will simplify to HLit. The "H" is the proton which can be given away to something else. The "Lit" is the rest of the weak acid molecule. There will be an equilibrium established when this acid dissolves in water. Taking the simplified version of this equilibrium:
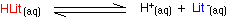
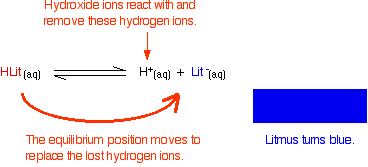
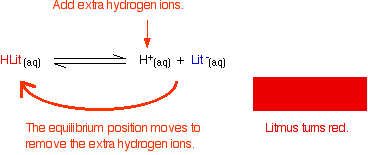
The un-ionised litmus is red, whereas the ion is blue. Now use Le Chatelier's Principle to work out what would happen if you added hydroxide ions or some more hydrogen ions to this equilibrium.
Adding hydroxide ions:
Adding hydrogen ions:
If the concentrations of HLit and Lit - are equal: At some point during the movement of the position of equilibrium, the concentrations of the two colors will become equal. The color you see will be a mixture of the two.

The reason for the inverted commas around "neutral" is that there is no reason why the two concentrations should become equal at pH 7. For litmus, it so happens that the 50 / 50 color does occur at close to pH 7 - that's why litmus is commonly used to test for acids and alkalis. As you will see below, that isn't true for other indicators.
Methyl orange
Methyl orange is one of the indicators commonly used in titrations. In an alkaline solution, methyl orange is yellow and the structure is:
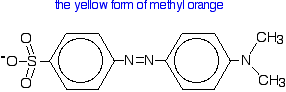
Now, you might think that when you add an acid, the hydrogen ion would be picked up by the negatively charged oxygen. That's the obvious place for it to go. Not so!
In fact, the hydrogen ion attaches to one of the nitrogens in the nitrogen-nitrogen double bond to give a structure which might be drawn like this:
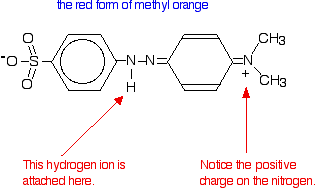
You have the same sort of equilibrium between the two forms of methyl orange as in the litmus case - but the colors are different.
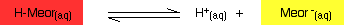
You should be able to work out for yourself why the color changes when you add an acid or an alkali. The explanation is identical to the litmus case - all that differs are the colors.
In the methyl orange case, the half-way stage where the mixture of red and yellow produces an orange color happens at pH 3.7 - nowhere near neutral. This will be explored further down this page.
Phenolphthalein
Phenolphthalein is another commonly used indicator for titrations, and is another weak acid.

In this case, the weak acid is colorless and its ion is bright pink. Adding extra hydrogen ions shifts the position of equilibrium to the left, and turns the indicator colorless. Adding hydroxide ions removes the hydrogen ions from the equilibrium which tips to the right to replace them - turning the indicator pink.
The half-way stage happens at pH 9.3. Since a mixture of pink and colorless is simply a paler pink, this is difficult to detect with any accuracy!
The pH range of indicators
The importance of pKind
Think about a general indicator, HInd - where "Ind" is all the rest of the indicator apart from the hydrogen ion which is given away:
\[HInd_{(aq)} \rightleftharpoons H^+_{(aq)} + Ind^-_{(aq)} \tag{1.6.1}\]
Because this is just like any other weak acid, you can write an expression for \(K_a\) for it. We will call it \(K_{ind}\) to stress that we are talking about the indicator.
\[ K_{ind} = \dfrac{[H^+][Ind^-]}{[HInd]} \tag{1.6.2}\]
Think of what happens half-way through the color change. At this point the concentrations of the acid and its ion are equal.
\[ [Ind^-] = [HInd] \tag{1.6.3}\]
In that case, they will cancel out of the Kind expression.
\[ K_{ind} = \dfrac{[H^+]\cancel{[Ind^-]}}{\cancel{[HInd]}} \tag{1.6.4}\]
\[ K_{ind} = [H^+] \tag{1.6.5}\]
You can use this to work out what the pH is at this half-way point. If you re-arrange the last equation so that the hydrogen ion concentration is on the left-hand side, and then convert to pH and pKind, you get:
\[ [H^+] = K_{ind} \tag{1.6.5}\]
\[ pH = -\log_{10} [H^+] = -\log_{10} K_{ind} = pK_{ind} \tag{1.6.6}\]
That means that the end point for the indicator depends entirely on what its pKind value is. For the indicators we've looked at above, these are:
| indicator | pKind |
|---|---|
| litmus | 6.5 |
| methyl orange | 3.7 |
| phenolphthalein | 9.3 |
The pH range of indicators
Indicators don't change color sharply at one particular pH (given by their pKind). Instead, they change over a narrow range of pH. Assume the equilibrium is firmly to one side, but now you add something to start to shift it. As the equilibrium shifts, you will start to get more and more of the second color formed, and at some point the eye will start to detect it. For example, suppose you had methyl orange in an alkaline solution so that the dominant color was yellow. Now start to add acid so that the equilibrium begins to shift. At some point there will be enough of the red form of the methyl orange present that the solution will begin to take on an orange tint. As you go on adding more acid, the red will eventually become so dominant that you can no longer see any yellow.
There is a gradual smooth change from one color to the other, taking place over a range of pH. As a rough "rule of thumb", the visible change takes place about 1 pH unit either side of the pKind value. The exact values for the three indicators we've looked at are:
| indicator | pKind | pH range |
|---|---|---|
| litmus | 6.5 | 5 - 8 |
| methyl orange | 3.7 | 3.1 - 4.4 |
| phenolphthalein | 9.3 | 8.3 - 10.0 |
The litmus color change happens over an unusually wide range, but it is useful for detecting acids and alkalis in the lab because it changes color around pH 7. Methyl orange or phenolphthalein would be less useful.
This is more easily seen diagramatically.
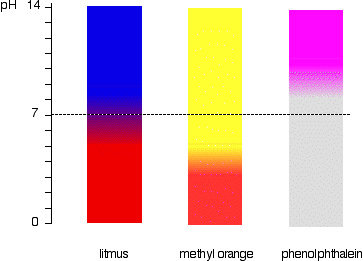
For example, methyl orange would be yellow in any solution with a pH greater than 4.4. It couldn't distinguish between a weak acid with a pH of 5 or a strong alkali with a pH of 14.
Choosing indicators for titrations
Remember that the equivalence point of a titration is where you have mixed the two substances in exactly equation proportions. You obviously need to choose an indicator which changes color as close as possible to that equivalence point. That varies from titration to titration.
Strong acid vs. strong base
The next diagram shows the pH curve for adding a strong acid to a strong base. Superimposed on it are the pH ranges for methyl orange and phenolphthalein.
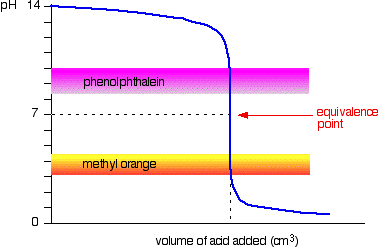
You can see that neither indicator changes color at the equivalence point. However, the graph is so steep at that point that there will be virtually no difference in the volume of acid added whichever indicator you choose. However, it would make sense to titrate to the best possible color with each indicator. If you use phenolphthalein, you would titrate until it just becomes colorless (at pH 8.3) because that is as close as you can get to the equivalence point. On the other hand, using methyl orange, you would titrate until there is the very first trace of orange in the solution. If the solution becomes red, you are getting further from the equivalence point.
Strong acid vs. weak base
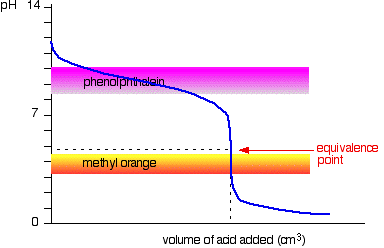
This time it is obvious that phenolphthalein would be completely useless. However, methyl orange starts to change from yellow towards orange very close to the equivalence point. You have to choose an indicator which changes color on the steep bit of the curve.
Weak acid vs. strong base
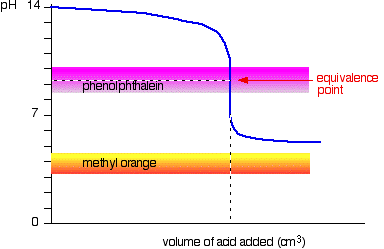
This time, the methyl orange is hopeless! However, the phenolphthalein changes color exactly where you want it to.
Weak acid vs. weak base
The curve is for a case where the acid and base are both equally weak - for example, ethanoic acid and ammonia solution. In other cases, the equivalence point will be at some other pH.
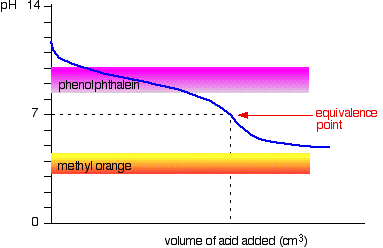
You can see that neither indicator is any use. Phenolphthalein will have finished changing well before the equivalence point, and methyl orange falls off the graph altogether. It may be possible to find an indicator which starts to change or finishes changing at the equivalence point, but because the pH of the equivalence point will be different from case to case, you can't generalise. On the whole, you would never titrate a weak acid and a weak base in the presence of an indicator.
Sodium carbonate solution and dilute hydrochloric acid
This is an interesting special case. If you use phenolphthalein or methyl orange, both will give a valid titration result - but the value with phenolphthalein will be exactly half the methyl orange one.
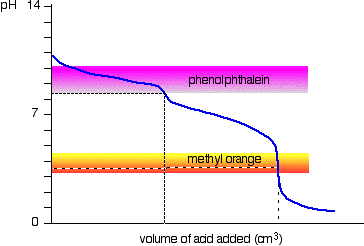
It so happens that the phenolphthalein has finished its color change at exactly the pH of the equivalence point of the first half of the reaction in which sodium hydrogencarbonate is produced.
\[ Na_2CO_{3(aq)} + HCl_{(aq)} \rightarrow NaCl_{(aq)} + NaHCO_{3(aq)} \tag{1.6.1}\]
The methyl orange changes color at exactly the pH of the equivalence point of the second stage of the reaction.
\[ NaHCO_{3(aq)} + HCl_{(aq)} \rightarrow NaCl_{(aq)} + CO_{2(g)} + H_2O_{(l)} \tag{1.6.2}\]


