Group Theory and its Application to Chemistry
- Page ID
- 1890
Group Theory is the mathematical application of symmetry to an object to obtain knowledge of its physical properties. What group theory brings to the table, is how the symmetry of a molecule is related to its physical properties and provides a quick simple method to determine the relevant physical information of the molecule. The symmetry of a molecule provides you with the information of what energy levels the orbitals will be, what the orbitals symmetries are, what transitions can occur between energy levels, even bond order to name a few can be found, all without rigorous calculations. The fact that so many important physical aspects can be derived from symmetry is a very profound statement and this is what makes group theory so powerful.
Introduction
To a fully understand the math behind group theory one needs to take a look at the theory portion of the Group Theory topic or refer to one of the reference text listed at the bottom of the page. Never the less as Chemist the object in question we are examining is usually a molecule. Though we live in the 21st century and much is known about the physical aspects that give rise to molecular and atomic properties. The number of high level calculations that need to be performed can be both time consuming and tedious. To most experimentalist this task is takes away time and is usually not the integral part of their work. When one thinks of group theory applications one doesn't necessarily associated it with everyday life or a simple toy like a Rubik's cube. A Rubik's cube is an a cube that has a \(3 \times 3\) array of different colored tiles on each of its six surfaces, for a total of 54 tiles. Since the cube exist in 3D space, the three axis are \(x\), \(y\), \(z\). Since the rubik's cube only allows rotation which are called operations, there are three such operations around each of the \(x\), \(y\), \(z\) axis.

Of course the ultimate challenge of a Rubik's cube is to place all six colors on each of the six faces. By performing a series of such operations on the Rubik's cube one can arrive at a solution (A link of a person solving a Rubik's cube1 in 10.4s with operations performed noted, the operations performed will not translate to chemistry applications but it is a good example of how symmetry operations arrive at a solution). The operations shown in the Rubik's cube case are inherent to the make up of the cube, i.e., the only operations allowed are the rotations along the x, y, z axis. Therefore the Rubik's cube only has x,y,z rotation operations. Similarly the operations that are specific to a molecule are dependent on its symmetry. These operations are given in the top row of the character table.
| \(C_{3v}\) | \(E\) | \(2C_3\) | \(3\sigma_v\) |
|
functions |
|---|---|---|---|---|---|
| \(A_1\) | +1 | +1 | +1 | \(z\) | \(x^2+y^2\), \(z^2\) |
| \(A_2\) | +1 | +1 | -1 | \(R_z\) | - |
| \(E\) | +2 | -1 | 0 | (\(x\), \(y\)) (\(R_x\), \(R_y\)) | (\(x^2-y^2\), \(xy\)) (\(xz\), \(yz\)) |
The character table contains a wealth of information, for a more detailed discussion of the character table can be found in Group Theory Theoretical portion of the chemWiki. All operations in the character table are contained in the first row of the character table, in this case \(E\), \(C_3\), & \(\sigma_v\), these are all of the operations that can be preformed on the molecule that return the original structure. The first column contains the three irreducible representations from now on denoted as \(\Gamma_{ir}\), here they are \(A_1\), \(A_2\) & \(E\). The value of the \(\Gamma_{ir}\) denotes what the operation does. A value of 1 represents no change, -1 opposite change and 0 is a combination of 1 & -1 (0’s are found in degenerate molecules. The final two columns Rotation and Translation represented by \(R_x\),\(R_y\), \(R_z\) & \(x\), \(y\), \(z\) respectively. Where R's refer to rotation about an axis and the \(x\), \(y\), \(z\) refers to a translation about an axis, the \(\Gamma_{ir}\) the each \(R_x\), \(R_y\), \(R_z\) & \(x\), \(y\), \(z\) term is the irreducible symmetry of a rotation or translation operation. Like wise the final column the orbital symmetries relates the orbital wavefunction to a irreducible representation.
Direct Products
This is a quick rule to follow for calculating Direct Products of irreproducible representations, such a calculation will be necessary for working through transition moment integrals. Following the basic rules given by the table given below. One can easily work through symmetry calculations very quickly.
| "Symmetric" \(\times\) "Symmetric" is "Symmetric" | "Symmetric" \(\times\) "AntiSymmetric" is "AntiSymmetric" | "AntiSymmetric" \(\times\) "Symmetric" is "AntiSymmetric" | "AntiSymmetric" \(\times\) "AntiSymmetric" is "Symmetric" |
|---|---|---|---|
| \(g \times g = g\) | \(g \times u = u\) | \(u \times g = u\) | \(u \times u = g\) |
| \( ' \times ' = '\) | \( ' \times '' = ''\) | \( '' \times ' = ''\) | \( '' \times '' = '\) |
| \(A \times A= A\) | \(A \times B= B\) | \(B \times A= B\) | \(B \times B= A\) |
Vibrations
All molecules vibrate. While these vibrations can originate from several events, which will be covered later, the most basic of these occurs when an electron is excited within the electronic state from one eigenstate to another. The Morse potential (electronic state) describes the energy of the eigenstate as a function of the interatomic distance. When an electron is excited form one eigenstate to another within the electronic state there is a change in interatomic distance, this result in a vibration occurring.
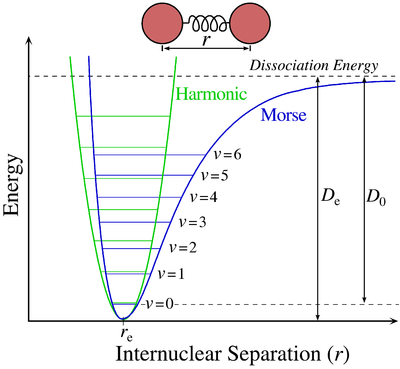
Vibrational energies arise from the absorption of polarizing radiation. Each vibrational state is assigned a \(\Gamma_{ir}\). A vibration occurs when an electron remains within the electronic state but changes from one eigenstate to another (The vibrations for the moment are only IR active vibrations, there are also Raman vibrations which will be discussed later in electronic spectroscopy), in the case of the Morse diagram above the eigenstates are denoted as \(\nu\). As you can see from the diagram the eigenstate is a function of energy versus interatomic distance.
To predicting whether or not a vibrational transition, or for that matter a transition of any kind, will occur we use the transition moment integral.
\[\int \Psi_i*\mu \Psi_f d\tau=\langle \Psi_i | \mu| \Psi_f \rangle\]
The transition moment integral is written here in standard integral format, but this is equivalent to Bra & Ket format which is standard in most chemistry quantum mechanical text (The \(\langle \Psi_i |\) is the Bra portion, \(| \Psi_f \rangle\) is the Ket portion). The transition moment operator \(\mu\) is the operator the couples the initial state \(\Psi_i\) to the final state \(\Psi_f\), which is derived from the time independent Schrödinger equation. However using group theory we can ignore the detailed mathematical methods. We can use the \(\Gamma_{ir}\) of the vibrational energy levels and the symmetry of the transition moment operator to find out if the transition is allowed by selection rules. The selection rules for vibrations or any transition is that is allowed, for it to by allowed by group theory the answer must contain the totally symmetric \(\Gamma_{ir}\), which is always the first \(\Gamma_{ir}\) in the character table for the molecule in question.
Symmetry
Let’s work through an example: Ammonia (\(NH_3\)) with a \(C_{3v}\) symmetry. Consequently, all of the properties contained in the \(C_{3v}\) character table above are pertinent to the ammonia molecule.
The principle axis is the axis that the highest order rotation can be preformed. In this case the z-axis pass through the lone pairs (pink sphere), which contains a \(C_3\) axis. The ?’s or mirror planes (\(\sigma_v\) parallel to z-axis & \(\sigma_h\) perpendicular to the z-axis). In ammonia there is no \(\sigma_h\) only three \(\sigma_v\)’s. The combination of \(C_3\) & \(\sigma_v\) leads to \(C_{3v}\) point group, which leads to the C3v character table.
The number of transitions is dictated by 3N-6 for non-linear molecules and 3N-5 for linear molecules, where N is the number of atoms. The 6 & the 5 derive from three translations in the x,y,z plan and three rotations also in the x,y,z plan. Where a linear molecule only has two rotations in the x & y plans since the z axis has infinite rotation. This leads to only 5 degrees of freedom in the rotation and translation operations. In the case of Ammonia there will be 3(4)-6=6 vibrational transitions. This can be confirmed by working through the vibrations of the molecule. This work is shown in the table below.
The vibrations that are yielded 2A1 & 2E (where E is doubly degenerate, meaing two vibration modes each) which total 6 vibrations. This calculation was done by using the character table to find out the rotation and translation values and what atoms move during each operation. Using the character table we can characterize the A1 vibration as IR active along the z-axis and raman active as well. The E vibration is IR active along both the x & y axis and is Raman active as well. From the character table the IR symmetries correspond to the x, y & z translations. Where the Raman active vibrations correspond to the symmetries of the d-orbitals.
Vibrational Spectroscopy
Infrared Spectroscopy
Infrared Spectroscopy (IR) measures the vibrations that occur within a single electronic state, such as the one shown above. Because the transition occurs within a single electronic state there is a variation in interatomic distance. The dipole moment is dictate by the equation.
\[ \vec{\mu} = \alpha\vec{E} \]
Where \( \vec{\mu} \) is the magnitude of dipole moment; \( \alpha \) is the polarizability constant (actually a tensor) & \( E \) is the magnitude of the electric field which can be described as the electronegitivity.3 Therefore when a vibration occurs within a single electronic state there is a change in the dipole moment, which is the definition of an active IR transition.
\[ \left ( \frac{\mathrm{d\mu} }{\mathrm{d} q} \right )_{eq} \neq 0 \]
In terms of group theory a change in the dipole is a change from one vibrational state to another, as shwon by the equation above. A picture of the vibrational states with respect ot the rotational states and electronic states is given below. In IR spectroscopy the transition occurs only from on vibrational state to another all within the same electronic state, shown below as B.
.jpg?revision=1&size=bestfit&width=572&height=414)
Electronic Transitions
When an electron is excited from one electronic state to another, this is what is called an electronic transition. A clear example of this is part C in the energy level diagram shown above. Just as in a vibrational transition the selection rules for electronic transitions are dictated by the transition moment integral. However we now must consider both the electronic state symmetries and the vibration state symmetries since the electron will still be coupled between two vibrational states that are between two electronic states. This gives us this modified transition moment integral:
Where you can see that the symmetry of the initial electronic state & vibrational state are in the Bra and the final electronic and vibrational states are in the Ket. Though this appears to be a modified version of the transition moment integral, the same equation holds true for a vibrational transition. The only difference would be the electronic state would be the same in both the initial and final states. Which the dot product of yields the totally symmetric representation, making the electronic state irrelevant for purely vibrational spectroscopy.
Raman
In Resonance Raman spectroscopy transition that occurs is the excitation from one electronic state to another and the selection rules are dictated by the transition moment integral discussed in the electronic spectroscopy segment. However mechanically Raman does produce a vibration like IR, but the selection rules for Raman state there must be a change in the polarization, that is the volume occupied by the molecule must change. But as far as group theory to determine whether or not a transition is allowed one can use the transition moment integral presented in the electronic transition portion. Where one enters the starting electronic state symmetry and vibrational symmetry and final electronic state symmetry and vibrational state, perform the direct product with the different M's or polarizing operators For more information about this topic please explore the Raman spectroscopy portion of the Chemwiki
Fluorescence
For the purposes of Group Theory Raman and Fluorescence are indistinguishable. They can be treated as the same process and in reality they are quantum mechanically but differ only in how Raman photons scatter versus those of fluorescence.
Phosphorescence
Phosphorescence is the same as fluorescence except upon excitation to a singlet state there is an interconversion step that converts the initial singlet state to a triplet state upon relaxation. This process is longer than fluorescence and can last microseconds to several minutes. However despite the singlet to triplet conversion the transition moment integral still holds true and the symmetry of ground state and final state still need to contain the totally symmetric representation.
Molecular Orbital Theory and Symmetry
Molecular Orbitals also follow the symmetry rules and indeed have their own ?ir. Below are the pi molecular orbitals for trans-2-butene and the corresponding symmetry of each molecular orbital.
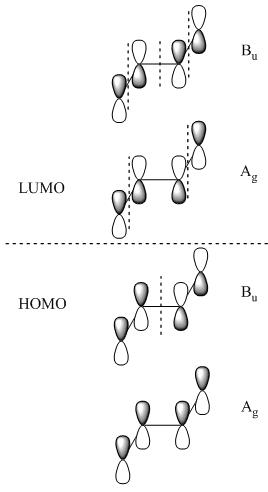
The ?ir of the molecular orbitals are created by simply preforming the operations of that molecule's character table on that orbital. In the case of trans-2-butene the point group is C2h, the operations are: E, C2, i & ?h. Each operation will result in a change in phase (since were dealing with p-orbitals) or it will result in no change. The first molecular orbital results in the totally symmetric representation, working through all four operations E, C2, i, ?h will only result in 1's meaning there is no change, giving the Ag symmetry state. These molecular orbitals also represent different electronic states and can be arranged energetically. Putting the orbital that has the lowest energy, the orbital with the fewest nodes at the bottom of the energy diagram and like wise working up form lowest energy to highest energy. The highest energy orbital will have the most nodes. Once you've set up your MO diagram and place the four pi electrons in the orbitals you see that the first two orbitals listed (lowest energy) are HOMO orbitals and the bottom two (highest energy) and LUMO orbitals. With this information if you have a transition from the totally symmetric HOMO orbital to the totally symmetric LUMO orbital the transition moment operator would need to have Ag symmetry (using the C2h) to give a result containing the totally symmetric representation.
These four molecular orbitals represent four different electronic states. So transitions from one MO into another would be something that is measured typically with UV-Vis spectrometer.
References and Further Reading
- Daniel Harris & Michael Bertolucci Symmetry and Spectroscopy New York, Dover Publications 1989 ($19.95), [Highly recommended, great text for explaining Group Theory for molecules and Application of Group Theory in various spectroscopy's]
- Albert Cotton Chemical Applications of Group Theory 3rd New York, Wiley Inter-science Publication 1990 ($148.50),[Mathematical approach to group theory in chemistry]
- Donald A. McQuarrie Quantum Chemistry Sausalito, University Science Books 1983 ($88.00) [Classic Quantum chemistry text very clear and thorough]
- Douglas Skoog, James Holler & Stanley Crouch Principles of Instrumental Analysis (6th ed) Thomson Brooks Cole 2007 ($170.04), [Covers basics of all types of analytical chemistry methods and theory]
Problems
- Follow the links above to Water, Ammonia and Benzene and work out the ?ir of the vibrations. Using the method laid out by the character table. (Follow the example of ammonia for help)
- From problem 1. work out what possible are the possible transition moment operators for each vibration.
- Work through the P-orbital molecular orbitals for cis-butadiene. (Note the conservation of "stuff", start by combining four p-orbitals and finish with four molecular orbitals) What is the point group? what are the ?ir of each MO? Finally how many vibrations are there for cis-butadiene and what are their ?ir.

