10: Quantum Fundamentals (Exercises)
- Page ID
- 41195
This is a set of problems that are organized to accompany the future "Physical Chemistry" textmap organized around Silbey et al. textbook.
Q10.3A
Calculate the energy per photon and the number of photons emitted per minute from
- 100-W yellow light bulb (\(λ= 550\;nm\))
- 1-kW microwave source (\(λ = 1\;cm\))
S10.3A
a. This is a two part problem. The first part is to calculate the energy per photon. The second part of to calculate the flux (number of photon/ time) from the power (energy/time).
- Energy per photon
\[E={hv}\] \[E=\dfrac{hc} {λ}\]
\[E=\dfrac{(6.634\times 10^{-34} J·s)·(3\times 10^8 m/s)} {550\times 10^9 m}\]
\[E=3.618\times 10^{-37} J\]
- Number of photons emitted per minute
\[\dfrac{100} {E}\ ·\dfrac{60s}{1 min}\]
\[\dfrac{100} {3.618\times 10^{-37} J}·\dfrac{60s}{1min}\]
\[=1.658\times 10^{40} \dfrac{photons}{min}\]
b. This is a two part problem. The first part is to calculate the energy per photon. The second part of to calculate the flux (number of photon/ time) from the power (energy/time).
- Energy per photon
\[E=\dfrac{(6.634\times 10^{-34} J·s)·(3\times 10^8 m/s)} {0.01 m}\]
\[E=1.99\times 10^{37}J\]
- Number of photons emitted per minute
\[\dfrac{1000} {1.99\times 10^{37} J}·\dfrac{60s}{1min}\]
\[=3.02\times 10^{-33} \dfrac{photons}{min}\]
Q10.3B
Calculate the energy per photon and the number of photons emitted per second from 200 W/s Short Wave UV Light with a wavelength of 280 nm.
S10.3B
Equation for frequency
\[\lambda \nu =c\]
and solve for \(\nu\)
\[v=\dfrac{c}{\lambda}\]
Equation for Energy
\[E=hv\]
Use the Equation for Frequency and Equation for Energy. Substitute \(\nu\) from Frequency Equation:
\[E=\dfrac{hc}{\lambda}\]
\[E=\dfrac{6.626 \times 10^{-34} Js \times 2.998 \times 10^{8} m/s }{2.8 \times 10^{-7}m}\]
\[E=7.07 \times 10^{-19} J\]
To get the number of Photons emitted, divide the total energy by the energy of a single photon.
\[\eta=\dfrac{\lambda \times E_{total}}{hc}\]
With the 200 Watts/s is converted to 200 J and wavelength is now in meters instead of Nanometers;
\[\eta=\dfrac{2.80 \times 10^{-7} m \times 200J}{6.626 \times 10^{-34} Js \times 2.998 \times 10^{8} m/s}\]
\[\eta=2.83 \times 10^{20} photons\]
Q10.3C
Calculate the energy per photon and the number of photons per second from
- a 60-W red light bulb (\(\lambda = 650 nm\))
- a 1.5-kW radiowave source (\(\lambda = 5cm\))
S10.3C
a) The energy of a photon is given by the equation \[E=\dfrac{hc}{\lambda}\] where h is Planck's constant and c is the speed of light.
Plugging in to this equation we get: \[E=\dfrac{(6.67\times10^{-34}J/s)(3.00\times10^8)}{650\times10^{-9}m}= 3.07\times10^{-19}J\]
To solve for the photons per second use \[Photons/sec=\dfrac{Power}{energy}\]
Power needs to be in Joules per second so \[60W=60J/s\]
Plugging in we get: \[\dfrac{60J/s}{3.07\times10^{-19}}=1.95\times10^{20}photons/s\]
b) Following the same method as part a, we get: \[E=\dfrac{(6.67\times10^{-34}J/s)(3.00\times10^8)}{0.05m}= 4.002\times10^{-24}J\]
and \[\dfrac{1500J/s}{4.002\times10^{-24}}=3.75\times10^{26}photons/s\]
Q10.3D
Calculate the energy per photon and the number of photons emitted per second from
- 10-W yellow light bulb (λ = 550 nm)
- a 500W microwave source (λ = 1 cm)
S10.3D
We know that Planck's constant \(h = 6.62607004\times 10^(-34) m^(2)*kg/s\) and the speed of light \(c = 2.99\times 10^8 m/s\).
The equation to calculate the energy is $$E=\dfrac{h*v}{λ}$$
Plug in all the data and we could get:
E(for λ = 550 nm) = \(3.602\times 10^(-19) J\)
E(for λ = 1 cm) = \(1.981\times 10^(-23) J\)
The power means the energy needed per second. P=E* # of particles. So the number of photons emitted are
n(for λ = 550 nm) \(= 10\,W/E = 2.776 \times 10^{19}\)
n(for λ = 1 cm) \(= 500\,W/E = 2.524 \times 10^{25}\)
Q10.3E
Prove that the three sp2 hybrid orbitals are directed at angles of 120 degree with respect to one another.
S10.03E
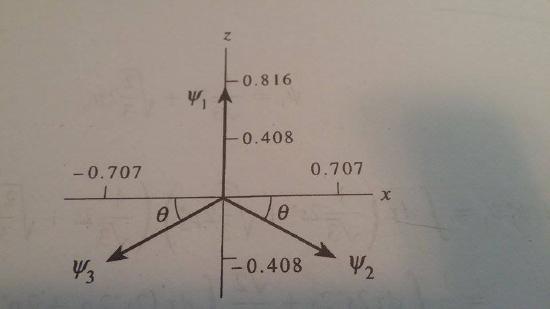
In this problem, because the s orbital is spherically symmetric, the directionality of the sp2 hybrid orbitals will be determined by their p-orbital character. The p-orbital characters of the sp2 hybrid orbitals are given by
\[\psi_1=\sqrt{2/3}*2*p_z\\ \psi_2=-\dfrac{1}{\sqrt(6)}*2*p_z+\dfrac{1}{\sqrt(2)}*2*p_x\\ \psi_3=-\dfrac{1}{\sqrt(6)}*2*p_z -\dfrac{1}{\sqrt(2)}*2*p_x\]
Therefore, one can represent these combinations of the p-orbitals as vectors with the appropriate projection on the x-axes and z axes.
Whence, we can evaluation theta by noting the equation right below, or θᵒ=30ᵒ. The angle between Ψ1 (and that between Ψ2and Ψ2) is 90ᵒ + 30ᵒ=120ᵒ. The angle between Ψ2 and Ψ3 must therefore be 360ᵒ-2(120ᵒ)) =120ᵒ.
\[\tan{\theta}=\dfrac{1}{\sqrt(6)}/\dfrac{1}{\sqrt(2)}=\dfrac{0.408}{0.707}\]
Q9.6
An ultraviolet photon (\(\lambda\)=142.7 nm) is absorbed by a hydrogen molecule at rest. What is the velocity of the hydrogen molecule? How much kinetic energy has been gained by the hydrogen molecule?
S9.6
If we assume that momentum is conserved then the hydrogen molecule at rest will have the same momentum from the photon determined by de Broglie's equation.
\[p=\dfrac {h}{\lambda} \]
Thus, the velocity of the hydrogen molecule is therefore (since it was initially at rest)
\[ v=\dfrac{p}{m}\]
or after inserting de Broglie's relations
\[v=\dfrac{h}{\lambda\,m}\]
\[v=\dfrac{ 6.626069 \times 10^{-34}\;kg \cdot m^2/s}{142.7 \times 10^{-9} m \times 1.6737236 \times 10^{-27} kg \times 2}\]
\[v=1.387 m/s\]
which means the kinetic energy is:
\[KE= \dfrac{1}{2} m v^2= \dfrac{1}{2} \times 1.6737236 \times 10^{-27} kg \times 2 \times (1.387 m/s)^2 = 3.22 \times 10^{-27}J\]
This calculation assumes none of the photon's linear momentum gets coupled into internal degrees of freedom for the hydrogen molecule (e.g., electron velocity or vibration or rotation).
Q10.6A
Calculate the wavelength of light emitted when an electron falls from the n=97 orbit to the n = 96 orbit of the hydrogen atom. Such species are known as high Rydberg atoms. They are detected in astronomy and are more and more studied in the laboratory.
S10.6A
\[ R_H = 1.097 \times\ 10^7 m^{-1}\]
\[1/\lambda = R_H \times \left ( \dfrac{1}{96^2} - \dfrac{1}{97^2} \right)\]
\[\lambda = 0.0410 \;m\]
Q10.6B
Rydberg atoms are excited atoms with more than one electron that possesses a very high principal quantum number. In a Bohr model, the radius of an electron orbit relies on the n value. If n=196, find the energy of the electron in the hydrogen atom.
S10.6B
\[E_n= \dfrac{-13.6eV}{n^2}\]
\[E_n=\dfrac{-13.6eV}{196^2} = 3.54 \times 10^{-4}\,eV\]
Q10.6C
Calculate the wavelength emitted when an electron falls from the n=50 orbit to the n=49 orbit of a hydrogen atom
S10.6C
\[E_n= -\dfrac{1.602\times 10^{-19} Joules}{n^2}\]
\[ \Delta E= -\dfrac{1.602\times 10^{-19}J}{50^2} - -\dfrac{1.602\times 10^{-19}J}{49^2}\]
\[ \Delta E= 2.642\times 10^{-24} Joules\]
\[ \Delta E= E_{photon}= h f ( h= 6.626\times 10^{-34} J*s, f=frequency (1/s)\]
\[ E_{photon} = \dfrac{2.642\times 10^{-24}J}{6.626\times 10^{-34} J*s}= 3.9873\times 10^9 s^{-1} \]
\[ \dfrac{c}{\lambda}=f\]
thus
\[\dfrac{3.00\times 10^8 m/s}{3.9873\times 10^9 s^{-1}}= \lambda=0.0752m\]
\[\lambda=0.0752m\]
Q10.6D
Species that transition at high energy levels, such as \(n=100\), are known as high Rydberg atoms. These are often used in astronomy. Calculate the frequency of light emitted when an electron falls from the \(n=99\) orbit to the \(n=96\) orbit of the hydrogen atom.
S10.6D
We know that the speed of light in vacumm is represented as
\[c=\lambda \nu\]
Additionally, we know that we can solve for the wavelength of an electron transition by
\[\dfrac{1}{\lambda} = R \left(\dfrac{1}{n_f^2} - \dfrac{1}{n_i^2} \right) \]
Combining these equations results in
\[\nu = \dfrac{c}{\lambda} = cR \left(\dfrac{1}{n_f^2} - \dfrac{1}{n_i^2}\right)\]
Using the known values, the frequency is represented as
\[\nu = 3\times 10^8 \dfrac{m}{s} \times \dfrac{1.097\times 10^7}{m}* \left(\dfrac{1}{96^2} -\dfrac{1}{99^2}\right)\]
With a final solution of
\[\nu = 2.1314\times 10^{10} Hz\]
Q10.6E
Calculate the wavelength of light emitted when an electron falls from the n = 50 orbit to the n = 49 orbit of the hydrogen atom. Such species are known as high Rydberg atoms. They are detected in astronomy and are more and more studied in the laboratory.
S10.6E
Rydberg equation is given by:
\[\dfrac{1}{\lambda}=R \times (\dfrac{1}{n_f^2}-\dfrac{1}{n_i^2})\label{1}\]
\[R=1.097 \times 10^7\dfrac{1}{m}\]
Given values in the problem are:
\[n_f = 49\]
\[n_i = 50\]
Plugging into the Rydberg equation results in:
\[\dfrac{1}{\lambda}=1.097 \times 10^7\dfrac{1}{m} \times (\dfrac{1}{49^2}-\dfrac{1}{50^2}) = 180.930\dfrac{1}{m}\]
To find the wavelength, invert the above value. This will give you:
\[\lambda = \dfrac{1}{180.930\dfrac{1}{m}} = .00553m\]
Q10.6F
Calculate the wavelength of light emitted when an electron falls from the n = 100 orbit to the n = 99 orbit of the hydrogen atom. Such species are known as Rydberg atoms. They are detected in astronomy and are more and more studied in the laboratory.
S10.6F
\[\dfrac{1}{\lambda} = R( \dfrac{1}{n_1^2}-\dfrac{1}{n_2^2})\]
\[\dfrac{1}{\lambda} = (1.097 \times 10^7)(\dfrac{1}{99^2}-\dfrac{1}{100^2})\]
\[\dfrac{1}{\lambda} = 22.27m^{-1}\]
\[\lambda = \dfrac{1}{22.27m^{-1}} =0.0449m\]
Q10.7
What is the de Broglie wavelength of an nitrogen molecule at room temperature (300K)?
S10.7
The de Broglie wavelength is given by \( \gamma = \dfrac{h}{p} = \dfrac{h}{mv}\)
For N2, a diatomic molecule, the velocity can be approximated by the root mean square speed with 5 degrees of freedom: thus \(\dfrac{1}{2}mv_{rms}^2 =\dfrac{5}{2}kT\)
\[ \gamma = \dfrac{h}{\sqrt{5mkT}}\]
\[ \gamma = \dfrac {6.626069 \times 10^{-34}\;kg \cdot m^2/s}{\sqrt{5(1.3806 \times 10^{-23}\: m^2kg/s^2\cdot K \times 300 K \times14.0067 amu \times 2\times 1.66054 \times 10^{-27} kg/amu)}}\]
\[\gamma= .02134 nm\]
Q10.8
What is the de Broglie wavelength of a free neutron with kinetic energy of 0.025 eV?
S10.8
Yet again, the de Broglie wavelength is given by \( \gamma = \dfrac{h}{p} = \dfrac{h}{mv}\).
For a free neutron, mn=1.674929 x 10-27 kg.
\[KE=\dfrac{1}{2}mv^2\]
\[v=\sqrt{\dfrac{KE\times 2}{ m}}\]
\[\gamma = \dfrac{h}{\sqrt{KE\times 2 m}}\]
\[\gamma = \dfrac{6.626 \times 10^{-34} kg \cdot m^2 /s}{\sqrt{0.025 eV (1.60218 \times 10^{-19} J/eV) \times 2\times 1.674929 \times 10^{-27}kg}}\]
\[\gamma = .1809nm\]
Q10.8A
If the wavelength of a x-ray photon in a x-ray photoelectron spectroscopy (XPS) instrument is 1.25 nm. Calculate the velocity of the electrons emitted from molecules in which the following work functions (e.g., binding energies): 25, 125, 425 eV.
S10.8A
Since \(\nu=(c/\lambda)\) Let's express the formula in the following form:
\[(1/2)m_ev^2=(hc)/\lambda-\phi\]
Where:
- m_e = mass of the electron
- h = Plank's constant
Then:
\[v^2=(2/m_e)(hc/\lambda)-\phi\]
For 25eV:
\(25eV=4.01\times 10^{-18} J\)
We now plug values inside the formula to calculate velocity:
\[v^2=\dfrac{2}{9.11\times 10^{-31} Kg}(\dfrac{6.63 \times10^{-34} J*s \times 3\times10 ^8 m/s}{1.25\times 10^{-9}m}-4.01\times 10^{-18}J)\]
From there we get the velocity:
\[v=1.84 \times 10^7 m/s\]
For 125eV :
\(125eV=2.00\times 10^{-17} J\)
We plug values inside the formula like before:
\[v^2=\dfrac{2}{9.11\times 10^{-31} Kg}(\dfrac{6.63 \times10^{-34} J*s \times 3\times10 ^8 m/s}{1.25\times 10^{-9}m}-2.00\times 10^{-17} J)\]
From there we obtain velocity:
\[v=1.75\times 10^7 m/s\]
For 450eV :
\(425eV=6.81\times 10^{-17} J\)
We plug for this values again:
\[v^2=\dfrac{2}{9.11\times 10^{-31} Kg}(\dfrac{6.63 \times10^{-34} J*s \times 3\times10 ^8 m/s}{1.25\times 10^{-9}m}-6.81\times 10^{-17} J)\]
We obtain velocity:
\[v=1.42\times 10^7 m/s\]
Q10.8B
Photoelectron spectroscopy utilizes the photoelectron effect to measure the binding energy of electrons in molecules and solids, by measuring the kinetic energy of the emitted electrons and using the relation between kinetic energy, wavelength, and binding energy:
\[\dfrac{1}{2}mv^2 = h \nu - \phi\]
One variant of this photoelectron spectroscopy is X-ray photoelectron spectroscopy. If the X-ray wavelength is 1 nm, calculate the velocity of electrons emitted from molecules in which the binding energies are 5, 50, &100 eV
S10.8B
First, solve the equation for velocity:
\[ v = \sqrt{\dfrac{ 2(h \nu - \phi)}{m}} \]
The givens are: $$ \lambda = 1 nm \text{ and } \phi = 5, 50, \text{&} 100 eV\]
There is no wavelength in the equation so we need:
\[ \nu = \dfrac{c}{\lambda} \text{ where } c=2.99 \text{x}10^8 \dfrac{\text{m}}{\text{s}} \text{ (speed of light) } \]
so we get:
\[ v = \sqrt{\dfrac{ 2(\dfrac{hc}{\lambda} - \phi)}{m}} \]
m is the mass of an electron: $$m=9.11\text{x}10^-31 \text{ Kg}\]
and $$hc=1.239\text{x}10^3eV nm\]
Plug in the numbers to the equation:
\[ v = \sqrt{\dfrac{ 2(\dfrac{1.239\text{x}10^3eV nm}{1 nm} - \phi)}{9.11\text{x}10^-31 \text{ Kg}}} \]
The units don't match so we need: $$1eV = 1.602\text{x}10^-19 J\]
So again, plug in the numbers:
\[ v = \sqrt{\dfrac{ 2(\dfrac{1.239\text{x}10^3eV nm}{1 nm} - \phi)*1.602\text{x}10^-19\dfrac{J}{eV}}{9.11\text{x}10^-31 \text{ Kg}}} \]
\[\text{For: } \phi=5 eV, v=2.083\text{x}10^7\]
\[\text{For: } \phi=50 eV, v=2.045\text{x}10^7\]
\[\text{For: } \phi=50 eV, v=2.001\text{x}10^7\]
Q10.8C
Calculate the velocity of electrons emitted from several different materials after the absorption of a photon with a wavelength of 10 nm, given the workfunctions of the materials are 200, 900, and 1000 eV respectively
S10.8C
\[\dfrac{1}{2}mv^2=h\nu-\phi\]
\[v=\sqrt{\dfrac{2(h\nu-\phi)}{m_e}}\]
\[c=\lambda\nu\]
\[\dfrac{c}{\lambda}=\nu\]
\[900pm \dfrac{1m}{1\times 10^{-10}pm}=9\times 10^{-10}m\]
\[200eV \dfrac{1.602\times 10^{-19}J}{1eV}=2.124\times 10^{-17}J\]
\[m_e=9.109\times 10^{-31}kg\]
\[h=6.626\times 10^{-34}J*s\]
\[v=\sqrt{\dfrac{2(\dfrac{(6.626\times 10^{-34}J*s)(2.998\times 10^{8})}{9\times 10^{-10}m}-2.124\times 10^{-17}J)}{9.109\times 10^{-31}kg}}\]
\[v=2.093\times 10^{7} \dfrac{m}{s}\]
\[900eV \dfrac{1.602\times 10^{-19}J}{1eV}=1.442\times 10^{-16}J\]
\[v=\sqrt{\dfrac{2(\dfrac{(6.626\times 10^{-34}J*s)(2.998\times 10^{8})}{9\times 10^{-10}m}-1.442\times 10^{-16}J)}{9.109\times 10^{-31}kg}}\]
\[v=1.296\times 10^{7} \dfrac{m}{s}\]
\[1000eV \dfrac{1.602\times 10^{-19}J}{1eV}=1.602\times 10^{-16}J\]
\[v=\sqrt{\dfrac{2(\dfrac{(6.626\times 10^{-34}J*s)(2.998\times 10^{8})}{9\times 10^{-10}m}-1.602\times 10^{-16}J)}{9.109\times 10^{-31}kg}}\]
\[v=1.153\times 10^{7} \dfrac{m}{s}\]
Q10.8E
Photoelectron spectroscopy utilizes the photoelectron effect to measure the binding energy of electrons in molecules and solids, by measuring the kinetic energy of the emitted electrons and using the relation in problem 10.7 (equation 1) between kinetic energy, wavelength, and binding energy. One variant of this photoelectron spectroscopy is X-ray photoelectron spectroscopy (XPS). If the X-ray wavelength is 0.250 nm, calculate the velocity of electrons emitted from the molecules in which the binding energies are 20, 200, and 2000 eV.
\[\dfrac{1}{2}mv^2 = h\nu-\phi \]
S10.8E
Solving for velocity (v) in equation 1 yields equation 2
\[v=\sqrt{\dfrac{2(h\nu-\phi)}{m_e}} \label{2}\]
where \(h\) is planck's constant, \(\nu\) is the frequency of the X-ray photon, \(\phi\) is the work function or binding energy, and \(m_e\) is the mass of an electron.
Substituting in the relationship between frequency and wavelength yields equation 3
\[v=\sqrt{\dfrac{2[h(\dfrac{c}{\lambda})-\phi]}{m_e}} \label{3}\]
where \(c\) is the speed of light and \(\lambda\) is the wavelength of the emitted electron.
Substituting in the values the binding energy of 20 eV yields
\[v=\sqrt{\dfrac{2[(6.626\times 10^{-34}m^2kg/s)(\dfrac{2.998\times 10^{8}m/s}{0.250\times 10^{-9}m})-20\;eV(\dfrac{1.602\times 10^{-19}J}{1\;eV})]}{9.109\times 10^{-31}kg}}\]
which reduces to
Q10.8F
Photoelectron spectroscopy utilizes the photoelectron effect to measure the binding energy of electrons in molecules and solids, by measuring the kinetic energy of the emitted electrons and using the relation in problem 10.7 between kinetic energy, wavelength, and binding energy. One variant of this is photoelectron spectroscopy is X-ray photoelectron spectroscopy (XPS). If the X-ray wavelength is 0.2 nm, calculate the velocity of electrons emitted from molecules in which the binding energies are 10, 100, and 500 eV.
S10.8F
The relation in problem 10.7: \[ \dfrac{1}{2}mv^2 = h \nu - \phi \]
Solve for velocity, v: \[ v = \sqrt{ \dfrac{2(h \nu - \phi)}{m}} \]
Given: $$ \lambda = 0.2 nm \text{ and } \phi = 10, 100, 500 eV \]
We know that \[ \nu = \dfrac{c}{\lambda} \text{ where } c=2.99E8 \dfrac{m}{s} \]
\[ me = 9.11E{-31} \]
\[ 1 eV = 1.602E-19J\]
\[ v = \sqrt{ \dfrac{2 \left( \dfrac{hc}{\lambda} \right) - \phi)*1.602E{-19} \dfrac{J}{eV}}{m}} \]
\[ \text{ when } \phi = 10 \text{ then } v = \sqrt{ \dfrac{2 \left( \dfrac{h*2.99E8 \dfrac{m}{s}}{0.2} \right) - 10)*1.602E{-19} \dfrac{J}{eV}}{9.11E{-31}}} \]
\[ = 4.66E7 \dfrac{m}{s} \]
\[ \text{ when } \phi = 100 \text{ then } v = \sqrt{ \dfrac{2 \left( \dfrac{h*2.99E8 \dfrac{m}{s}}{0.2} \right) - 100)*1.602E{-19} \dfrac{J}{eV}}{9.11E{-31}}} \]
\[ = 4.63E7 \dfrac{m}{s}\]
\[ \text{ when } \phi = 500 \text{ then } v = \sqrt{ \dfrac{2 \left( \dfrac{h*2.99E8 \dfrac{m}{s}}{0.2} \right) - 500)*1.602E{-19} \dfrac{J}{eV}}{9.11E{-31}}} \]
\[ = 4.48E7 \dfrac{m}{s} \]
Q10.9
Calculate the de Broglie wavelengths of the following:
- A 1-g bullet with velocity 300 m s-1
- A 10-6-g particle with velocity 10-6 m s-1
- A 10-10-g particle with velocity 10-10 m s-1
- An H2 molecule with energy of 3/2kT at T = 20 K
S10.9
De Broglie wavelength:
\[λ = \dfrac{h}{mv} = \dfrac{h}{p}\]
where p = momentum, h = Plank's constant (6.626 x 10-34 Js), v = velocity, m = mass
(a) \[λ = \dfrac{6.626 \times 10^{-34} \space Js}{(1 \times 10^{-3} \space kg)(300 \space m/s)} = 2.21 \times 10^{-33} \space m\]
(b) \[λ = \dfrac{6.626 \times 10^{-34} \space Js}{(10^{-6} \times 10^{-3} \space kg)(10^{-6} \space m/s)} = 6.626 \times 10^{-19} \space m\]
(c) \[λ = \dfrac{6.626 \times 10^{-34} \space Js}{(10^{-10} \times 10^{-3} \space kg)(10^{-10} \space m/s)} = 6.626 \times 10^{-10} \space m\]
(d) k is the Boltzmann constant (1.38 x 10-23 J/K)
\[E = \dfrac{3}{2}kT = (\dfrac{3}{2})(1.38 \times 10^{-23} \space J/K)(20 \space K)\ = 4.14 \times 10^{-22} \space J\]
\[E = \dfrac{1}{2} mv^2 = \dfrac{p^2}{2m}\]
\[p= \sqrt{2mE}\]
Mass of an H2 molecule is 3.35 x 10-27 kg
\[\lambda = \dfrac{6.626 \times 10^{-34} \space Js}{\sqrt{2(3.35 \times 10^{-27} \space kg)(4.14 \times 10^{-22} \space J)}}\ = 3.1 \times 10^{-9} \space m\]
Q10.9A
Protons are accelerated by a 1500 V potential drop.
- Calculate the kinetic energy of a proton once accelerated.
- Calculate the de Broglie wavelength of the accelerated proton.
S10.9A
(a) To find kinetic energy we first must calculate the velocity of the accelerated proton. We first find the difference in potential energy using the potential difference and the charge of a proton:
\[\Delta P=P_b-P_a=q(V_b-V_a)=(1.6\times 10^{-19})(-1500)=-2.4\times 10^{-16} J \]
We can find the Kinetic energy by:
\[\Delta K=-\Delta P=+2.4\times 10^{16} J \]
(b) By using the equation for kinetic energy we can rearrange to solve for the velocity:
\[\Delta K = \dfrac{1}{2}mv^2\]
Becomes:
\[v=\sqrt{\dfrac{2\Delta K }{m_p}} = \sqrt{\dfrac{2(2.4\times 10^{16} J) }{1.67\times 10^{-27}}} = 5.36\times 10^5 ms^{-1} \]
Now we solve for the wavelength \(\lambda\) \[\lambda = \dfrac{h}{m_pv} = 2.11\times 10^{-14} cm^{-1}\]
Q10.9B
Electrons are accelerated by a 666-V potential drop.
- Calculate the de Broglie wavelength.
- Calculate the wavelength of the X-rays that could be produced when these electrons strike a solid.
S10.9B
Electron charge (C)
\[1.602 \times 10^{-19}\]
Electron mass (kg)
\[9.11 \times 10^{-31}\]
Planck's constant (J s)
\[6.626 \times 10^{-34}\]
Determining the electron's charge
\[E_{electron} = E_{charge} \times V_{drop}\]
\[E_{electron} (J) = E_{charge} \times V_{drop} = 1.066 \times\ 10^{-16}\]
\[E_{electron} = \dfrac{1}{2} mv^{2} = \dfrac{1}{2}\dfrac{p^{2}}{m}\]
Determining wavelength
\[\lambda = \dfrac{h}{p} = \dfrac{h}{\sqrt{2mE}}\]
a. de Broglie wavelength (m)
\[\lambda = \dfrac{h}{p} = \dfrac{h}{\sqrt{2mE}} = 4.75 \times 10^{-11}\]
b. wavelength of X-rays that could be produced when these electrons strike a solid (m)
\[E_{photon} = \dfrac{hc}{\lambda_{photon}} \]
\[\lambda_{photon} = 2.81 \times 10^{-9}\]
Q10.C
A 2000-V potential drop accelerates electrons.
- Find the de Broglie wavelength.
- Find the frequency of the X-rays that might be produced when these electrons strike a solid
Potentially useful information:
- charge of an electron \(e=-1.602\times 10^{-16} \;J\)
- mass of an electron \(m_e= 9.109\times 10^{-31} \;kg\)
- Planck's constant \(h=6.626\times 10^{-34} \;Js\)
- speed of light \(c=3\times 10^{8} \dfrac{m}{s}\)
S10.9C
(a) De Broglie's wavelength can be found using the equation:
\[\lambda=\dfrac{h}{mv}=\dfrac{h}{p}\]
Since the voltage drop is equal to the amount of electrical energy per Coulomb,
\[E=eV=(1.602\times 10^{-16} \;C)(2000 \;V)\]
We also know the electron has kinetic energy, so
\[E=\dfrac{1}{2} m_ev^2\]
We know that,
\[p=m_ev\]
So,
\[E=\dfrac{p^2}{2m_e}\]
Now, rearranging to get an expression for p,
\[p=\sqrt{2m_eE}\]
Substituting this expression for p into the de Broglie wavelength equation,
\[\lambda=\dfrac{h}{\sqrt{2m_eE}}=\dfrac{(6.626\times 10^{-34} \;Js)}{\sqrt{(2)(9.109\times 10^{-31} \;kg)(1.602\times 10^{-16} \;C)(2000 \;V)}} \]
Calculating,
\[\lambda=2.743\times 10^{-11} \;m\]
(b) We can use an equation for energy of a photon in order to find the wavelength of the X-rays.
\[E=\dfrac{hc}{\lambda}\]
Rearranging,
\[\lambda=\dfrac{hc}{E}=\dfrac{(6.626\times 10^{-34} \;Js)(3\times 10^{8} \dfrac{m}{s})}{(1.602\times 10^{-16} \;C)(2000 \;V)}\]
\[\lambda=6.2041\times 10^{-10} \;m\]
Now that we the X-ray's wavelength, we can find the frequency using
\[c=\lambda\nu\]
Solving for \(\nu\),
\[\nu=\dfrac{c}{\lambda}=\dfrac{(3\times 10^{8} \dfrac{m}{s})}{6.2041\times 10^{-10} \;m}\]
\[\nu=4.836\times 10^{17} \;Hz\]
Q10.9D
Initially stationary electrons are accelerated by a 150-V potential drop.
- Calculate the De Broglie Wavelength.
- Calculate the wavelength of the X-Rays that could be produced when these electrons strike a solid.
S10.9D
kinetic energy of an electron is given by
\[m=9.11 \times 10^{-31}kg\]
\[e=1.6 \times 10^{-19}C\]
\[E_{electron}=eV=(1.6 \times 10^{-19})(150) = 2.4 \times 10^{-17} J\]
\[E=\dfrac{1}{2}mv^2\label{1A}\]
Solve for v:
\[v=\sqrt{\dfrac{2KE}{m}}\label{2A}\]
\[v=7.25\times 10^{6}\dfrac{m}{s}\]
\[\lambda=\dfrac{h}{p}=\dfrac{h}{mv}\label{3A}\]
\[\lambda = 1.00\times 10^{-10} m\]
(b)
\[E_{photon} = \dfrac{hc}{\lambda_{photon}}\label{4A}\]
where \(c\) is the speed of light
\[c = 3.00\times 10^{8} \dfrac{m}{s}\]
\[\lambda_{photon} = 8.28*10{-9} m\]
Q9.10
The lifetime of a molecule in a certain electronic state is 10-10 s. What is the uncertainty in energy of this state? Give the answer in J and in J mol-1.
S9.10
\[\Delta E \Delta t \geq \dfrac{h}{4 \pi}\]
\[\Delta E \geq \dfrac{h}{4 \pi \Delta t} \geq \dfrac{6.63 \times 10^{-34} \space J \cdot s}{4 \pi (10^{-10} \space s)}\]
\[\Delta E \geq 5.27 \times 10^{-25} \space J\]
\[\Delta E \times (6.022 \times 10^{23} \space 1/mol) \geq 0.318 \space J mol^{-1}\]
Q10.10b
An ultraviolet photon (λ= 120 nm) from a helium gas discharge tube is absorbed by a hydrogen molecule which is at rest. Since momentum is conserved, what is the velocity of the hydrogen molecule after absorbing the photon? What is the translational energy of the hydrogen molecule in Jmol-1.
S10.10b
Use momentum to find the velocity of the hydrogen molecule:
\[p=\dfrac{h} {λ}\]
\[ λ=120×10^{-9} meters\]
\[h= 6.55×10^{-34}\]\[m_{H_2}=3.32×10^{-27} kg\]
\[p= \dfrac{6.55×10^{-34}Js}{120×10^{-9} meters}=5.46×10^{-27} \dfrac{kg*m}{s}\]
\[v=\dfrac{p}{m_{H_2} }\]
\[\dfrac{5.46×10^{-27}\dfrac{kg*m}{s}}{120×10^{-9} meters}=1.63\dfrac{m}{s}\]
Translational Energy is the same as kinetic energy, so:
\[KE=\dfrac{1}{2}mv^2\]
\[(\dfrac{1}{2})(3.32×10^{-27} kg)(1.63\dfrac{m}{s})^2 = 8.82×10^{-27} Joules\]
In molar terms:
\[(8.82×10^{-27} Joules)(6.022×10^{23} mol^{-1}) = 5.31×10^{-3} \dfrac{Joules}{mol}\]
Q10.11a
- Find the de Broglie wavelength of N2 at 450K.
- How does this relate to the average distance between N2 molecules in gas phase at 1 atm at 450K?
S10.11a
(a)The wavelength of a particle is given by de Broglie's equation:
\[λ = \dfrac{h}{mv}\]
For N2,
\[m ≈ 2*14 amu, 1 amu ≈1.66\times 10^{-27} kg \]
v is defined by the relationship between kinetic energy and temperature:
Into de Broglie's equation:
\[λ = \dfrac{6.626\times 10^{-34}*m^{2}*kg*s^{-1}}{(4.648\times 10^{-26}kg)(6.33\times 10^{2}m*s^{-1})}\]
\[λ=2.26\times 10^{-9}m\]
(b)The average distance between molecules is the radius of the volume per molecule, i.e. the full volume divided by the total number of molecules in the sample. Assuming 1 mole, or 6.0221x1023 molecules of N2, we can use the Ideal Gas Law to find the radius:
\[PV=nRT, n=1,R=82.058\dfrac{cm^{3}*atm}{K*mol} , P=1\] \[V_{mol}=\dfrac{(82.058\dfrac{cm^{3}*atm}{K*mol})(450K)(1mol)}{1atm}\] \[V_{mol}=3.693\times 10^{4}*cm^{3}\]
\[V_{N_2}=\dfrac{3.693\times 10^{4}*cm^{3}}{6.0221\times 10^{23}}\] \[V_{N_2}=6.13\times 10^{-26}*m^{3}\] \[V=\dfrac{4\pi r^3}{3}\] \[V=\dfrac{4\pi r^3}{3}=6.13\times 10^{-26}*m^{3}\] \[r=2.44\times 10^{-9}m\]
The radius of the volume per molecule begins at the center of each molecule, so we may substract a bond length to the radius to approximate a better answer. The N2 bond length is of the magnitude of 1x10-10m, which would reduce our answer only slightly to be 2.34x10-9m.
The two values are very close given that the calculations of the distance between molecules were rough estimations.
Q10.11C
What is the de Broglie wavelength of a oxygen molecule moving at the average speed at 40 °C? Compare this to the average distance between oxygen molecules in a gas at 1 atm and 40 C.
S10.11C
Start with the equating the kinetic energy to the temperature via the equipartition relationship.
\[\dfrac{1}{2} mv^2=\dfrac{3}{2} kT\]
Solving for velocity, we get:
\[v=\sqrt{\dfrac{3kT}{m}}\]
Now, we need the molecular mass of oxygen (since we are using \(k\)instead or \(R\). Tthe molar mass of \(O_2\) is 32 and to get calculate the molecular mass, we multiply 32 with the mass of a Proton \(1.672\times 10^{27}\):
\[m= (32)(1.672\times 10^{27} kg\]
\[m=5.352\times 10^{-26}\]
This is a single molecule of oxygen so Boltzman constant (k) will be used instead of R the gas constant and 313 K as out temperature.
\[v=\sqrt{\dfrac{3(1.38\times 10^{-23}m^2 kg s^{-1})(313 K)}{5.352\times 10^{-26}kg}}\]
\[v=4.92\times 10^{2} m s^{-1}\]
Then we use the de broglie wave equation \[\lambda=\dfrac{h}{p}\] where momentum (p) is p=mv.
where \(h\) is the planck's constant :
\[\lambda=\dfrac{6.626\times 10^{-34} m^2 kg s^{-1}}{(492 m s^{-1}) (5.352\times 10^{-26} kg)}\]
\[\lambda=2.516\times 10^{-11} m \]
or 25 pm
Assuming that we have 1 cubic meter vessel at 1 barr at 313 K we need to calculate the moles in the vessel per cubic meter.
\[PV=nRT\]
\[n=\dfrac{PV}{RT}\]
\[n=\dfrac{(1 atm)(1 m^3)}{(8.31 JK^{-1} mol^{-1}) (313 K)}\]
\[n= 3.844\times 10^{-4}\ m^3 mol^{-1}\]
Taking the cube root of n will give us n = 0.0727 meters \(mol^{-1}\)
Q10.11D
Which homonuclear diatomic molecule has a de Broglie wavelength of \(12.09 pm\) at room temperature? Assume room temperature is \(25°C\).
S10.11D
Begin with the de Broglie thermal wavelength:
\[\Lambda= \sqrt{\dfrac{h^2}{2\pi mk_BT}}\]
where
h is the Planck constant
m is the mass
\(k_B\) is the Boltzmann constant
T is the temperature.
Also, convert picometers to meters and Celsius to Kelvin before plugging in any values.
To determine the molecule, we will plug in our knowns and solve for the mass(m), not to be confused with the distance in meters:
\[1.209 \times 10^{-11} \;m = \dfrac{6.626 \times 10^{-34}\;J*s}{\sqrt{(2 \pi)(1.38 \times 10^{-23}\;J/K)(m)(298K)}}\]
Now, it is pretty simple algebra to solve for the mass in kg
\[m = 1.1627 \times 10^{-25}\;kg\]
To identify the molecule, let's convert to the more familiar atomic mass units (amu)
\[m = 1.1627 \times 10^{-25}\;kg \times (\dfrac{1 amu}{1.66 \times 10^{-27}\;kg}) ≈ 70.04 amu\]
Remember, this molecule is homonuclear diatomic, so if \(70 amu\) doesn't indicate \(Cl_2\) then dividing by 2 might make it more clear
\[\dfrac{70 amu}{2} = 35 amu \]
Thus, the molecule must consist of two chlorine atoms.
Q10.12A
What is the de Broglie wavelength of a thermal neutron at 350 K? A thermal neutron has the kinetic energy equal to the average kinetic energy of a thermalized monotonic gas (i.e., described by the Maxwell-Boltzmann distribution).
S10.12A
The de Broglie wavelength is determined by
\[\lambda = {\dfrac{h}{p}} = {\dfrac{h}{m \upsilon}}\label{1}\]
where \(p \) is momentum, \(m\) is mass, and \(\upsilon\) is velocity.
A neutron's velocity is determined by
\[\upsilon = (\dfrac{3 k_B T}{m})^{1/2} \label{2}\]
Substituting equation \((2)\) into \((1)\) we get
\[\lambda = \dfrac{h}{(3 m k_B T)^{1/2}}\label{3}\]
where \(h\) is Planck's constant and \(k_B\) is the Boltzmann constant.
We can now solve for our de Broglie wavelength by plugging in \(T=350 K\) and \(m=1.67 \times 10^{-27} kg\) (mass of a neutron)
\[\lambda = \dfrac{6.626 \times 10^{-34} m^2 kg/s}{(3 (1.67 \times 10^{-27} kg) (1.38 \times 10^{-23} J/K) (350 K))^{1/2}} = 1.455 \times 10^{-10} m\]
Q10.12B
What is the (a) temperature and (b) De Broglie wavelength of a thermal proton (proton in thermal equilibrium with its surroundings) with an average Kinetic Energy of 4.14E-16 J?
S10.12B
(a) The average Kinetic Energy (KE) of a proton is related to its temperature by
\[\overline{KE} = \dfrac{3}{2}kT\]
where k is the Boltzmann constant (\(k = 1.38E{-23} m^{2}kg^{1}s^{-2}K^{-1}\)) and \(T\) is in Kelvins.
\[T = \dfrac{2}{3}k\overline{KE}\] \[T = 2.00\times 10^7 K\]
This is one approximation of the temperature at the suns core.
(b) The De Broglie wavelength is given b the following formula
\[\lambda = \dfrac{h}{p}\]
where \(h\) is plancks constant (\(h = 6.63E{-34} m^{2}kg^{1}s^{-1}\)), \(p\) is the momentum of the particle, and \(m_p\) is the mass of a proton
\[m_p\overline{KE} = \dfrac{1}{2}p^2\]
\[p = \sqrt{(2m_p\overline{KE})}\]
and therefore
\[\lambda = \dfrac{h}{\sqrt{2m_p\overline{KE}}}\]
Q10.12c
What is the De Broglie wavelength of a thermal neutron at STP? Express your answer in SI units.
S10.22c
A thermal neutron has an average kinetic energy of \[KE=\dfrac{3}{2}kT\] where k is Boltzmann’s constant (1.3806×10−23J/K). The De Broglie wavelength lambda is given by: \[\lambda =\dfrac{h}{p}\] where p is the particle's momentum and h is Planck's constant \(h=6.62607004\cdot 10^{-34}J\cdot s\)
But,
\[p=(2m\times KE)^{\dfrac{1}{2}}\]
For a neutron \(m_{n}=1.67492747\cdot 10^{-27}kg,\)and STP means \(T=273.15K.\) So:
\[p=[2\times(1.67492747\cdot 10^{-27}kg)\times\dfrac{3}{2}\times(1.3806\cdot 10^{-23}J/K)\times273.15K]^{\dfrac{1}{2}}\] \[p=4.3518\cdot 10^{-24}kg\cdot m/s\] \[\lambda =\dfrac{h}{p}=1.5226\cdot 10^{-10}m\]
Q10.13c
Calculate the de Broglie wavelengths of the following:
- a) A honeybee (0.1 g) flying at 20 mph.
- b) An electron traveling at 2.00% of the speed of light.
S10.13c
For a honeybee of mass 0.1 g flying at 20 mph, velocity and momentum are
"\[v=\left(\dfrac{20 mi}{1 hr}\right)\left(\dfrac{1610 m}{1 mi}\right)\left(\dfrac{1 hr}{3600 s}\right)=8.94 \dfrac{m}{s}\]
\[p=mv=(0.0001 kg)(8.94\dfrac{m}{s})=8.94\times 10^{-4} kg\dfrac{m}{s}\]
The de Broglie wavelength is "\[\lambda=\dfrac{h}{p}, \text{ where h is } 6.626\times 10^{-34} J.s\]
Therefore, \[\lambda=\dfrac{h}{p}=\dfrac{6.626\times 10^{-34}}{8.94\times 10^{-4}}=7.41\times 10^{-31}m\]
"\[\text{ for an electron with mass of } 9.109\times 10^{-31} kg\text { traveling at 2.00% of the speed of light, velocity and momentum are}\]
\[v=(0.0200)(2.998\times 10^8)=5.99\times 10^6 m.s^{-1}\]
\[p=m_ev=(9.109\times 10^{-31})(8.99\times 10^6)=5.46\times 10^{-24} kg.m.s^{-1}\]
Therefore, \[\lambda=\dfrac{h}{p}=\dfrac{6.626\times 10^{-34}}{5.46\times 10^{-24}}=1.21\times 10^{-10} m=121 pm\]
Q10.13d
Calculate the de Brogile wavelengths of the following :
- a 1g bullet with velocity 300 m · s-1
- a 10-6 g bullet with velocity 10-6 m · s-1
- a 10-10g bullet with velocity 10-10 m · s-1
- a H2 molecule with energy of \[ \dfrac{3}{4}KT \] at T=20 K
S10.13d
(a)
\[1g = 10^{-3}\;kg \]
\[p = mv = 10^{-3}\times300 = 0.3\; kg\cdot m\cdot s^{-1} \]
The de Broglie wavelength is
\[\lambda = \dfrac{h}{p} = \dfrac{6.626 × 10^{-34}}{0.3 } =2.208× 10^{-33}\;kg\cdot m\cdot s^{-1}\]
(b)
\[10^{-6} = 10^{-9}\;kg \]
\[p = mv = 10^{-9}\times10^{-6} = 10^{-15}\; kg\cdot m\cdot s^{-1} \]
The de Broglie wavelength is
\[\lambda = \dfrac{h}{p} = \dfrac{6.626 × 10^{-34}}{10^{-15} } = 6.626 × 10^{-19}\;kg\cdot m\cdot s^{-1}\]
(c)
\[10^{-10} = 10^{-13}\;kg \]
\[p = mv = 10^{-13}\times10^{-10} = 10^{-23}\; kg\cdot m\cdot s^{-1} \]
The de Broglie wavelength is
\[\lambda = \dfrac{h}{p} = \dfrac{6.626 × 10^{-34}}{10^{-23} } = 6.626 × 10^{-11}\;kg\cdot m\cdot s^{-1}\]
(d) The energy of H2 is \[E=\dfrac{3}{4}K\times 20 =15K\] \[E=\dfrac{p^2}{2m}\] \[p=\sqrt{2mE}\] \[p=\sqrt{30mK}\]
\[\lambda = \dfrac{h}{p} = \dfrac{6.626 × 10^{-34}}{\sqrt{30mK}} = 6.626 × 10^{-34}\times\sqrt{30mK}\;kg\cdot m\cdot s^{-1}\]
Q10.13e
Calculate the de Broglie wavelengths of the following:
- a .8g bullet with velocity 340ms-1.
- a 10-5g particle with velocity 10-5ms-1.
- a 10-8g particle with velocity 10-8ms-1.
- an electron moving with velocity 4.8*106ms-1.
S10.13e
De Broglie wavelength:
\[\lambda = \dfrac{h}{P} = \dfrac{h}{mv}\]
where P = momentum, h = Plank's constant (6.626*10-34Js), v = velocity, m = mass
a)
\[\lambda = \dfrac{6.626 \times 10^{-34} \text{Js}}{(.8 \times 10^{-3} \text{Kg})(340 \text{m/s})} = 2.44 \times 10^{-33} \text{m}\]
b)
\[\lambda = \dfrac{6.626 \times 10^{-34} \text{Js}}{(10^{-5} \times 10^{-3} \text{Kg})(10^{-5} \text{m/s})} = 6.626 \times 10^{-21} \text{m}\]
c)
\[\lambda = \dfrac{6.626 \times 10^{-34} \text{Js}}{(10^{-8} \times 10^{-3} \text{Kg})(10^{-8} \text{m/s})} = 6.626 \times 10^{-15} \text{m}\]
b)
\[\lambda = \dfrac{6.626 \times 10^{-34} \text{Js}}{(9.1 \times 10^{-31} \text{Kg})(4.8^{6} \text{m/s})} = 1.52 \times 10^{-10} \text{m}\]
Mass of an electron is 9.1*10-31 kg.
Q10.13f
What is the de Broglie wavelength for a proton traveling at 1000 times the speed of sound?
S10.13f
The mass of a proton is given by:
\[m{_{p}}=1.672*10^{-27}\]
The speed of sound is given by:
\[v{_{sound}}=340.29 m/s\]
This gives us a value of momentum as follows:
\[p=(v{_{sound}}*1000)*m{_{p}}=340.29*1000*1.672*10^{-27}=5.6896*10^{-22}\]
Planck's constant is:
\[h=6.626*10^{-34}\]
This gives us the de Broglie wavelength as follows:
\[\lambda =\dfrac{h}{p}=\dfrac{6.626*10^{-34}}{5.6896*10^{-22}}=1.1646*10^{-12}m\]
Q9.14
For a particle in a one-dimension box, the ground-state wavelength is
\[\phi = \left(\dfrac{2}{a}\right)^{1/2}sin{\dfrac{\pi x}{a}}\]
- What is the probability that the particle is in the right-hand half of the box?
- What is the probability that the particle is in the middle third of the box?
S9.14
(a) The right-hand half of the box is \(\dfrac{L}{2} \leq x \leq L\)
\[ P\left(\dfrac{L}{2} ≤ x ≤ L\right)=\int_{\dfrac{L}{2}}^{L} \psi^*(x) \psi(x)dx \\ =\int_{\dfrac{L}{2}}^{L}\dfrac{2}{L}\sin^2{\dfrac{\pi x}{L}}dx=\dfrac{2}{L}\dfrac{1}{2}\int_{\dfrac{L}{2}}^{L}(1-\cos{\dfrac{2\pi x}{L}})dx=\\ \dfrac{1}{L}x\Biggr\rvert_{\dfrac{L}{2}}^{L} +\dfrac{1}{L}\dfrac{L}{2\pi}(-\sin{\dfrac{2\pi x}{L}})\Biggr\rvert_{\dfrac{L}{2}}^{L} \\= \dfrac{1}{L}L-\dfrac{1}{L}\dfrac{L}{2}-\dfrac{1}{2\pi}\sin{\dfrac{2\pi L}{L}}+\dfrac{1}{2\pi}\sin{\dfrac{2\pi L}{2L}}=\\ 1-\dfrac{1}{2}-\dfrac{1}{2\pi}\sin{2\pi}+\dfrac{1}{2\pi}\sin{\pi} \\= \dfrac{1}{2} - \dfrac{1}{2n\pi} (0)+\dfrac{1}{2n\pi} 0 = \\ \dfrac{1}{2} - 0 + 0 \\ = \dfrac{1}{2} = 0.50 \]
(b) The middle third of the box is \(\dfrac{L}{3} \leq x \leq \dfrac{2L}{3}\)
\[ P\left(\dfrac{L}{3} ≤ x ≤ \dfrac{2L}{3}\right)\\=\int_{\dfrac{L}{3}}^{\dfrac{2L}{3}} \psi^*(x) \psi(x)dx\\=\int_{\dfrac{L}{3}}^{\dfrac{2L}{3}}\dfrac{2}{L}\sin^2{\dfrac{\pi x}{L}}dx=\dfrac{2}{L}\dfrac{1}{2}\int_{\dfrac{L}{3}}^{\dfrac{2L}{3}}(1-\cos{\dfrac{2\pi x}{L}})dx=\\ \dfrac{1}{L}x\Biggr\rvert_{\dfrac{L}{3}}^{\dfrac{2L}{3}} +\dfrac{1}{L}\dfrac{L}{2\pi}(-\sin{\dfrac{2\pi x}{L}})\Biggr\rvert_{\dfrac{L}{3}}^{\dfrac{2L}{3}}= \dfrac{1}{L}\dfrac{2L}{3}-\dfrac{1}{L}\dfrac{L}{3}-\dfrac{1}{2\pi}\sin{\dfrac{2\pi 2L}{3L}}+\dfrac{1}{2\pi}\sin{\dfrac{2\pi L}{3L}}=\\ \dfrac{2}{3}-\dfrac{1}{3}-\dfrac{1}{2\pi}\sin{\dfrac{4\pi}{3}}+\dfrac{1}{2\pi}\sin{\dfrac{2\pi}{3}}= \dfrac{1}{3} - \dfrac{1}{2n\pi} (-\dfrac{\sqrt{3}}{2})+\dfrac{1}{2n\pi} \dfrac{\sqrt{3}}{2} = \\ \dfrac{1}{3} + \dfrac{1}{2\pi} \sqrt{3} = \dfrac{1}{3} + 0.28 = 0.61 \]
Q10.15
For a particle in a one-dimensional box, the ground-state wavefunction is
\[\phi = \sqrt{\dfrac{2}{a}} sin(\dfrac{\pi x}{a})\]
- What is the probability that the particle is in the left quarter of the box?
- What is the probability that the particle is between 3/8 the length of the box and 5/8 the length of the box?
S10.15
a) The probability that the particle can be found in the first quarter of the box is found using:
\[ prob = \int^{ \dfrac{a}{4} }_0 |\phi|^2\,dx = \int^{\dfrac{a}{4}}_0 \dfrac{2}{a}sin^2 ( \dfrac{\pi x}{a}),dx \]
The solution to this integral requires the trig identity
\[ sin^2 (x) = \dfrac{1}{2}(1 - cos(2x) ) \]
Using this and computing the integral results in the solution:
\[ prob = \dfrac{1}{2} - \dfrac{1}{2\pi} \]
b) The probability that the particle can be found between the 3/8 and 5/8 the length of the box is found in the exact same manner, this time changing the bounds to
\[ \int^{ \dfrac{5}{8}a }_{\dfrac{3}{8}a} |\phi|^2\,dx \]
The solution is:
\[ prob = \dfrac{1}{4} \]
Q10.19
- Determine the energy levels for for n = 1,2, and 3 in a potential well that is 0.29 nm wide and has infinite barriers on either side.
- If an electron makes a transition from n = 1 to n = 3, what is the wavelength of emitted radiation.
Q10.17C
What are the results of operating on the following functions with following two operators:
- \( \hat{A} = \dfrac{d}{dx}\) and
- \( \hat{B} = \dfrac{d^2}{dx^2}\)
- \(3e^{-cx^3}\)
- \(\cos(4ax^2)\)
- \(e^{i^2kx^3}\)
S10.17C
a)
- Apply Operator: \[ \dfrac{d(3e^{-cx^3})}{dx}\]Take derivative of the whole function by multiplying the exponential by the derivative of its superscript: \[ -9cx^{2}e^{-cx^{3}} \]
- Apply Operator: \[ \dfrac{d^2(3e^{-cx^3})}{dx^2}\]Which is the same as: \[ \dfrac{d(\dfrac{d(3e^{-cx^3})}{dx})}{dx}\]Or: \[ \dfrac{d(-9cx^{2}e^{-cx^{3}})}{dx}\]And take the derivative the same way as before: \[ 27c^{2}x^{4}e^{-cx^{3}} \]
b)
- Apply Operator: \[ \dfrac{d(\cos(4ax^2))}{dx}\]Take derivative with respect to cosine first, and then with respect to the function within the cosine: \[ -8ax\sin(4ax^{2}) \]
- Apply Operator: \[ \dfrac{d^2(\cos(4ax^2))}{dx^2}\]Which is the same as: \[ \dfrac{d(\dfrac{d(\cos(4ax^2))}{dx})}{dx}\]Or: \[ \dfrac{d(-8ax\sin(4ax^{2}))}{dx}\] And take the derivative the same way as before, except now you need the Chain Rule. Take the derivative of the 'x' term before the sine and multiply by the sine function. Then take the derivative of the sine function and multiply by the 'x' function: \[ -8a\sin(4x^{2})-64a^{2}x^{2}\cos(4ax^{2}) \]
c)
- Apply Operator: \[ \dfrac{d(e^{i^2kx^3})}{dx}\]Take derivative of the whole function by multiplying the exponential by the derivative of its superscript. Note that the 'i' within the superscript refers to the imaginary number 'i':\[ -3kx^{2}e^{-kx^{3}} \]
- Apply Operator: \[ \dfrac{d^2(e^{i^2kx^3})}{dx^2}\]Which is the same as: \[ \dfrac{d(-3kx^{2}e^{-kx^{3}})}{dx}\]And take the derivative the same way as before, except now you need the Chain Rule. Take the derivative of the 'x' term before the exponential and multiply by the exponential function. Then take the derivative of the exponential function and multiply by the 'x' function: \[ -6kxe^{-kx^{3}}+9k^2x^4e^{-kx^3} \]And finally, simplify:\[3kxe^{-kx^{3}}(3kx^3-2)\]
Q10.17D
What are the results of operating on the following functions with the operator
\[\dfrac{d}{dx} \]
and the operator
\[\dfrac{d^2}{dx^2} \]
- \(\ln{(-ax^2)} \)
- \(tan({bx}) \)
- \(e^{(ikx)} \)
Which functions are eigenfunctions of these operators? What are the corresponding eigenvalues?
S10.17D
(a) First operate on the function using the operators given.
\(\dfrac{d}{dx} \) \(\ln{(-ax^2)} \) = \(\dfrac{2}{x}\)
\(\dfrac{d^2}{dx^2} \) \(\ln{(-ax^2)} \) = \(-\dfrac{2}{x^2}\)
(b)
\(\dfrac{d}{dx} \) \(tan({bx}) \) = \(bsec^2({bx}) \)
\(\dfrac{d^2}{dx^2} \) \(tan({bx}) \) = \(b^2sec^2({bx})tan({bx})\)
(c)
\(\dfrac{d}{dx} \) \(e^{(ikx)} \) = \(ike^{(ikx)} \)
\(\dfrac{d^2}{dx^2} \) \(e^{(ikx)} \) = \(-k^2e^{(ikx)} \)
Now to determine if the functions are eigenfunctions of these operators, we take the result after operating on the function, and if that result is a constant times the original function, then the function is a eigenfunction of that operator. In this case, For (a), x is not a constant, so it is not an eigenfunction. For (b), although b is a constant, it is not that constant times a constant for both \(\dfrac{d}{dx} \) and \(\dfrac{d^2}{dx^2} \). For (c), we do indeed have an eigenfunction, \(ik\) is a constant, times its original function \(e^{(ikx)} \). The same goes for \(\dfrac{d^2}{dx^2} \), we have a constant \(-k^2\) times the original function \(e^{(ikx)} \). The eigenvalues are the constants of these functions, \(ik\) and \(-k^2\) for \(\dfrac{d}{dx} \) \(e^{(ikx)} \) and \(\dfrac{d^2}{dx^2} \) \(e^{(ikx)} \) respectfully.
Q10.17E
What are the results of operating on the following functions with the operator \(\dfrac{d}{dx}\) and \(\dfrac{d^2}{dx^2}\) :
- \(e^\dfrac{-Zx^2}{a_0}\)
- \(\cosh bk\)
- \(kx\)
S10.17E
a) \( \dfrac{d}{dx}\left(e^\dfrac{-Zx^2}{a_0}\right) \)
\[ = \dfrac{-2zx}{a_0} e^\dfrac{-Zx^2}{a_0} \]
Since \( \dfrac{-2zx}{a_0}\) isn't constant this isn't an eigenfunction for this operator
\(\dfrac{d^2}{dx^2}\left(e^\dfrac{-Zx^2}{a_0}\right) \)
\[ = \dfrac{d}{dx}\left (\dfrac{-2zx}{a_0} e^\dfrac{-Zx^2}{a_0}\right) \]
\[ = \dfrac{-2zx}{a_0} e^\dfrac{-Zx^2}{a_0} + \dfrac{4z^2x^2}{a^2_0} e^\dfrac{-Zx^2}{a_0} \]
\[ = \left( \dfrac{-2zx}{a_0} + \dfrac{4z^2x^2}{a^2_0}\right) e^\dfrac{-Zx^2}{a_0}\]
Since the \(\left( \dfrac{-2zx}{a_0} + \dfrac{4z^2x^2}{a^2_0}\right) \) isn't constant this isnt an eigenfunction for this operator either
b) \( \dfrac{d}{dx}\left(\cosh bx\right) \)
\[ = b \sinh bx\]
Not an eigenfunction since we didn't get our original function back for this operator
\[ \dfrac{d^2}{dx^2}\left(\cosh bx\right) \]
\[ = \dfrac{d}{dx}\left(b \sinh bx\right) \]
\[ = b^2 \cosh bx \]
For this operator \( b^2 \) is the eigenvalue and \( \cosh bx\) is the eigenfunction
c) \( \dfrac{d}{dx}\left(kx\right) \)
\[ = k = \dfrac{1}{x} kx \]
Since we get a variable term this isnt an eigenfunction for this operator.
\[ \dfrac {d^2}{dx^2}\left(kx\right) = 0 \]
For this operator \(0\) is our eigenvalue and \(kx\) is our eigenfunction.
Q10.19A
- Calculate the energy levels for n = 1, 3, and 5 for an electron in a potential well of width 0.50 nm with infinite barriers on either side.
- If an electron makes a transition from n = 3 to n = 1, what will be the wavelength of the emitted radiation?
S10.19A
(a)
Solve by using the following general equation for the expectation value for energy for a particle in a 1D box:
\[E_n = \dfrac{n^2 h^2}{8 m L^2}\]
Solve for n = 1, n = 2, and n = 3 where \(h = 6.626\times 10^{-34} \;J \cdot s\), \(m = 9.109\times 10^{-31} \;kg\), and \(L = 5.0\times 10^{-10} \;m\):
\[E_1 = \dfrac{(1)^2 (6.626\times 10^{-34}\;J-s)^2}{8 (9.109\times 10^{-31}\;kg) (5.0\times 10^{-10}\;m)^2} = 2.41\times 10^{-19} \;J\]
\[E_3 = \dfrac{(3)^2 (6.626\times 10^{-34}\;J-s)^2}{8 (9.109\times 10^{-31}\;kg) (5.0\times 10^{-10}\;m)^2} = 2.17\times 10^{-18} \;J\]
\[E_5 = \dfrac{(5)^2 (6.626\times 10^{-34}\;J-s)^2}{8 (9.109\times 10^{-31}\;kg) (5.0\times 10^{-10}\;m)^2} = 6.02\times 10^{-18} \;J\]
(b)
Find the energy emitted by finding the difference between E3 and E1:
\[E_3 - E_1 = 2.17\times 10^{-18} \;J - 2.41\times 10^{-19} \;J = 1.93\times 10^{-18}\;J\]
Find the wavelength of the energy emitted by the Planck-Einstein relation:
\[\Delta E = h\nu\]
\[\Delta E = h(\dfrac{c}{\lambda})\]
\[\lambda = 1.03\times 10^{-7}\;m\]
Q10.20A
For a helium atom in a one-dimensional box calculate the value of the quantum number of the energy level for which the energy is equal to 5/4 kT at 30°C for:
- a box \(10^{-3}\;m\) long,
- a box \(10^{-5}\;m\) long, and
- a box \(10^{-9}\;m\) long.
S10.20A
For parts (a)-(c) we need to rewrite the following equation in terms of n:
\[E_n=\dfrac{n^{2}h^{2}}{8mL^{2}}\]
Solving for n we get:
\[n=\sqrt{\dfrac{E_n8mL^{2}}{h^{2}}}\]
where
\[E_n=\dfrac{5}{4}(1.38\times10^{-23}m^{2}kgs^{-2}K^{-1})(303K)=5.23\times10^{-21}J\]
Plug in each value of L in meters and solve
- \[n=\sqrt{\dfrac{(5.23\times10^{-21}J)8(6.647\times10^{-27}kg)(10^{-3})^{2}}{(6.67\times10^{-34}J/s)^{2}}}=2.5\times10^{7}\]
- \[n=\sqrt{\dfrac{(5.23\times10^{-21}J)8(6.647\times10^{-27}kg)(10^{-5})^{2}}{(6.67\times10^{-34}J/s)^{2}}}=2.5\times10^{5}\]
- \[n=\sqrt{\dfrac{(5.23\times10^{-21}J)8(6.647\times10^{-27}kg)(10^{-9})^{2}}{(6.67\times10^{-34}J/s)^{2}}}=25\]
Q10.20B
For a helium atom in a one-dimensional box calculate the value of the quantum number of the energy level for which the energy is equal to 2 kT at 25ºC.
- box \(1\; nm\) long
- box \(10^^{-6}\;m\) long
- box \(10^{-2}\;m\) long
S10.20B
\[En= \dfrac{n^2·\hbar·pi^2}{2·m·L^2}\ = \dfrac{n^2·h^2}{8·m·L^2}\]
\[En= 2kT\] \[k= Boltzmanns constant\ 1.38\times 10^-23 \dfrac{m^2·kg^2}{s^2 K}\]
a) \[2·1.38·10^-23·298 = \dfrac{n^2·(6.634\times 10^-34)^2}{8·2·(1.66\times 10^-27\times 10^-18)}\]
\[8.22\times 10^-21 = n^2·1.675\times 10^-23\]
\[n^2= 490.746\]
\[n=22.15\]
b) \[2·1.38·10^-23·298 = \dfrac{n^2·(6.634\times 10^-34)^2}{8·2·(1.66\times 10^-27\times 10^-12)}\]
\[8.22\times 10^-21 = n^2·1.675\times 10^-29\]
\[n^2= 490736341\]
\[n=22152.569\]
c)
\[2·1.38·10^-23·298 = \dfrac{n^2·(6.634\times 10^-34)^2}{8·2·(1.66\times 10^-27\times 10^-4}\]
\[8.22\times 10^-21 = n^2·1.675\times 10^-37]
\[n^2= 4.9\times 10^16\]
\[n=221525696.2\]
Q10.20C
For a Helium atom in one-dimensional box calculate the value of the quantum number of the energy level for which the energy is equal to 2KT at 25 ℃
- for a box 10 nm long,
- for a box \(2\times 10^{-6} m\) long,
- for a box \(5\times 10^{-2} m\) long.
S10.20C
T = 25℃ = 298.15 K. K = 1.381\times 10^(-23) JK^(-1). So the energy equals to E = 6.176*10(-21) J.
we know that $$E_n=\dfrac{h^2*n^2}{8*M_e*a^2}$$ where Me is the electron weight and a is the length of the box.
To get the energy level, we use the function and plug in all the data. $$M_e=9.109\times 10^(-31)Kg\]
\[n=\dfrac{a}{h}\sqrt{8*M_e*E_n}\]
Then we could get:
- n = 0.3202
- n = 640.3361
- n = 16008000
Q10.20D
For a helium atom in a one-dimensional box, calculate the quantum number for the wavefunctions with the energies equal to the average kinetic energy of a thermalized monotonic gas (e.g, 3/2 kT) for a box 1 nm long at -100 oC, 0 oC, and 100 oC.
S10.20D
Use Energy Equation:
\[E_{n}=\dfrac{n^{2}h^{2}}{8mL^{2}}\]
Substitute Average Energy from Question for En
\[\dfrac{3}{2} \times kT=\dfrac{n^{2}h^{2}}{8mL^{2}}\]
Solve this equation for n:
\[n=\sqrt{\dfrac{12kTmL^{2}}{h^{2}}}(1)\]
Convert 1 nm to _ m
\[L=10^{-9} m\]
Convert each temperature from oC to K
Then plug in the numbers into the Equation (1) to find the quantum number for the different temperatures:
\[T=173K\]
\[n=\sqrt{\dfrac{12 \times (1.38 \times 10^{-23}J/K) \times 173K \times 6.65 \times 10^{-27}kg \times atom^{-1} \times 1^{-18}m^{2}}{(6.626 \times 10^{-34})^{2}Js}}\]
\[n=21\]
\[T=273K\]
\[n=\sqrt{\dfrac{12 \times (1.38 \times 10^{-23}J/K) \times 273K \times 6.65 \times 10^{-27}kg \times atom^{-1} \times 1^{-18}m^{2}}{(6.626 \times 10^{-34})^{2}Js}}\]
\[n=26\]
\[T=373K\]
\[n=\sqrt{\dfrac{12 \times (1.38 \times 10^{-23}J/K) \times 373K \times 6.65 \times 10^{-27}kg \times atom^{-1} \times 1^{-18}m^{2}}{(6.626 \times 10^{-34})^{2}Js}}\]
\[n=31\]
S10.20e
Now, Notice the lowest Energy molecular orbital is effectively equal to the 1s_x orbital. This is a core atomic orbital and is not involved in the bonding. (Recall that bonding orbitals involve the valence shell electrons, which for the X atom are in the orbitals with the highest n quantum number. Which is n XH3
Q10.22a
Calculate the degeneracies of the first 3 levels of a particle in a 4D box of length L
S10.22a
\[ E(n_x,n_y,n_z,n_w)=\dfrac{\pi^2\hbar^2}{2mL^2}(n_x^2+n_y^2+n_z^2+n_w^2)\]
since all dimensions have the same length, all dimensions have the same contribution to energy
Finding the first, second, and third lowest energy levels:
\[E_1=E(1,1,1,1)\]
Only 1 possibility, non-degenerate for E1
\[E_2=E(2,1,1,1)=E(1,2,1,1)=E(1,1,2,1)=E(1,1,1,2)\]
4 possibilities, 4-fold degenerate for E2
\[E_3=E(2,2,1,1)=E(2,1,2,1)=E(2,1,1,2)=E(1,2,2,1)=E(1,2,1,2)=E(1,1,2,2)\]
6 possibilities, 6-fold degenerate for E3
Q10.22b
Compare the process of calculating the degeneracy within a 2-D box and 3-D box.
S10.22b
A particle in a 3-D box has many more degeneracies in comparison to a particle in a 2-D box. The size of a 2-D box is L x L, which gives a ground state energy of 2E0. 2-D Box: \[E= E_0(n^{2}_x+n^{2}_y)\]
A 3-D cubic box has a size of L x L x L, and \[E=E_0(n^{2}_x+n^{2}_y+n^{2}_z)\]
Q10.22c
Calculate the degeneracies of the first four levels for a particle in a cubical box.
S10.22c
Write the energy as a sum of energies. For a cubical box, there are three separable modes. In a cube each are proportional to \(1/a^2\).
The three quantum numbers are: \(N_x , N_y , N_z\)
Energy goes like \((N_x)^2 + (N_y)^2 +(N_z)^2\)
So, the lowest energy level is (1,1,1), Energy = 3 Non-degenerate
Next, (2,1,1) = (1,2,1) = (1,1,2), Energy = 6 Threefold Degenerate
Next (2,2,1) = (2,1,2) = (1,2,2), Energy = 9 Threefold Degenerate
Finally (2,2,2), Energy = 12 Non-degenerate
Q10.22d
For the first five energy levels of a particle in a cubic box, calculate the degeneracies.
S10.22d
We know that degenerate energy can be represented as
\[E = \dfrac{h^2}{8ma^2} (N_x^2 + N_y^2 + N_z^2)\]
Where \(N_x\), \(N_y\), and \(N_z\) each represent a different quantum number.
Using M as a simplifying term,
\[E_0 = \dfrac{h^2}{8ma^2}\]
We get Energy levels at 3\(E_0\), 6\(E_0\), 9\(E_0\), 11\(E_0\), and 12\(E_0\). These are represented in Figure 1, with their degeneracy values indicated.
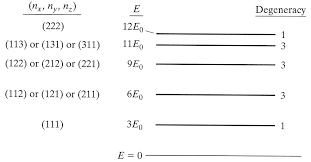
Figure 1
Q10.22e
Calculate the degeneracies of the first two levels for a particle in a square box.
S10.22e
The equation for energy is given by
\[E_{n_x,n_y} = \dfrac{h^2}{8mL^2}(n_x^{2} + n_y^{2})\]
For the first level \[n_x,n_y = 1,1\] results in
\[E_{1,1} = \dfrac{h^2}{8mL^2}(4 + 1)\]
\[E_{1,1} = \dfrac{h^2}{4mL^2}\]
For the second level \[n_x,n_y = 2,1\]results in
\[E_{2,1} = \dfrac{h^2}{8mL^2}(4 + 1)\]
\[E_{2,1} = \dfrac{5h^2}{8mL^2}\]
Q10.22f
Calculate the degeneracies of the first three levels for a particle in a cubical box.
S10.22f
\[E_{n_x,n_y,n_z} = \dfrac{h^2}{8mL^2}(n_x^{2} + n_y^{2} + n_z^{2})\]
\[E_{1,1,1} = \dfrac{h^2}{8mL^2}(1 + 1 +1)\]
\[E_{1,1,1} = \dfrac{3h^2}{8mL^2}\]
\[E_{2,1,1} = \dfrac{h^2}{8mL^2}(4 + 1 +1)\]
\[E_{2,1,1} = \dfrac{3h^2}{4mL^2}\]
\[E_{1,2,1} = \dfrac{h^2}{8mL^2}(1 + 4 +1)\]
\[E_{1,2,1} = \dfrac{3h^2}{4mL^2}\]
Q10.24a
Check the normalization of \(\psi_2\) and \(\psi_3\) for the harmonic oscillator and show they are orthogonal.
S10.24a
The wave function for \(\psi_2\) is
\[ \psi_2(x) = (\dfrac{\alpha}{4\pi})^{1/4} (2\alpha x^2 - 1)e^{-\alpha x^2/2} \label{10.24a.1}\]
where \( \alpha = \dfrac{\sqrt{k\mu}}{\hbar} \) and \(\mu\) is the reduced mass
and the normalization condition is
\[ \int_{-\infty}^{\infty} \psi_2^*(x) \psi_2(x) dx = 1 \label{10.24a.2}\]
Since all values are real, substituting in \( \psi_2(x) \) yields
\[ \int_{-\infty}^{\infty} (\dfrac{\alpha}{4\pi})^{1/2} (2\alpha x^2 - 1)^2 e^{-\alpha x^2} dx = 1 \label{10.24a.3}\]
which can be expanded to
\[ (\dfrac{\alpha}{4\pi})^{1/2} [ 4\alpha^2 \int_{-\infty}^{\infty} x^4 e^{-\alpha x^2} dx -4\alpha \int_{-\infty}^{\infty} x^2 e^{-\alpha x^2} dx + \int_{-\infty}^{\infty} e^{-\alpha x^2} dx ] = 1 \label{10.24a.4}\]
Using the Gaussian integral
\[\int_{-\infty}^{\infty}x^{2n}e^{-\alpha x^2} dx=\dfrac{1*3*5* ... *(2n-1)}{2^n\alpha^n} \sqrt{\dfrac{\pi}{a}} \]
Equation \ref{10.24a.4} becomes
\[ (\dfrac{\alpha}{4\pi})^{1/2} \; [ \; 4\alpha^2(\dfrac{3}{4\alpha^2})\sqrt{\dfrac{\pi}{\alpha}} - 4\alpha \dfrac{1}{2\alpha} \sqrt{\dfrac{\pi}{\alpha}} + \sqrt{\dfrac{\pi}{\alpha}} \; ] \; = 1 \label{10.24a.5}\]
which reduces to
\[ \sqrt{\dfrac{\alpha}{4\pi}}\sqrt{\dfrac{\pi}{\alpha}} \; [3-2+1] = 1 \label{10.24a.6}\]
and further to
\[ \dfrac{1}{2} \; [2] = 1 \label{10.24a.7}\]
leading to the true statement
\[ 1 = 1 \]
therefore, \(\psi_2\) is normalized.
The wave function for \(\psi_3\) is
\[ \psi_3(x) = (\dfrac{\alpha^3}{9\pi})^{1/4} (2\alpha x^3 - 3x)e^{-\alpha x^2/2} \label{10.24a.8}\]
and the normalization condition is
\[ \int_{-\infty}^{\infty} \psi_3^*(x) \psi_3(x) dx = 1 \label{10.24a.9}\]
Since all values are real, substituting in \( \psi_3(x) \) yields
\[ \int_{-\infty}^{\infty} (\dfrac{\alpha^3}{9\pi})^{1/2} (2\alpha x^3 - 3x)^2 e^{-\alpha x^2} dx = 1 \label{10.24a.10}\]
which can be expanded to
\[ (\dfrac{\alpha^3}{9\pi})^{1/2} [ 4\alpha^2 \int_{-\infty}^{\infty} x^6 e^{-\alpha x^2} dx -12\alpha \int_{-\infty}^{\infty} x^4 e^{-\alpha x^2} dx + 9\int_{-\infty}^{\infty} x^2 e^{-\alpha x^2} dx ] = 1 \label{10.24a.11}\]
Using the same Gaussian integral as before equation 11 becomes
\[ (\dfrac{\alpha^3}{9\pi})^{1/2} \; [ \; 4\alpha^2(\dfrac{15}{8\alpha^3})\sqrt{\dfrac{\pi}{\alpha}} - 12\alpha \dfrac{3}{4\alpha^2} \sqrt{\dfrac{\pi}{\alpha}} + 9\dfrac{1}{2\alpha}\sqrt{\dfrac{\pi}{\alpha}} \; ] \; = 1 \label{10.24a.12}\]
which reduces to
\[ \sqrt{\dfrac{\alpha^3}{9\pi}}\sqrt{\dfrac{\pi}{\alpha}}\dfrac{1}{\alpha} \; [\dfrac{15}{2}-\dfrac{18}{2}+\dfrac{9}{2}] = 1 \label{10.24a.13}\]
and further to
\[ \dfrac{1}{3} \; [3] = 1 \label{10.24a.14}\]
leading to the true statement
\[ 1 = 1 \]
therefore, \(\psi_3\) is normalized.
The orthogonality requirement for \(\psi_2\) and \(\psi_3\) is
\[ \int_{-\infty}^{\infty} \psi_2^*(x) \psi_3(x) dx = 0 \label{10.24a.15}\]
Since all values are real, the order is irrelevant so substituting in \( \psi_2(x) \) and \( \psi_3(x) \) yields
\[ \int_{-\infty}^{\infty} (\dfrac{\alpha^4}{36\pi^2})^{1/4} ( 2\alpha x^2 - 1)(2\alpha x^3 - 3x) e^{-\alpha x^2} dx = 0 \label{10.24a.16}\]
which can be expanded to
\[ \dfrac{\alpha}{\sqrt{6\pi}} [ 4\alpha^2 \int_{-\infty}^{\infty} x^5 e^{-\alpha x^2} dx -8\alpha \int_{-\infty}^{\infty} x^3 e^{-\alpha x^2} dx + 3\int_{-\infty}^{\infty} x e^{-\alpha x^2} dx ] = 0 \label{10.24a.17}\]
and since each of these integrals have integrands that are odd functions, the value of each of them is 0. The equation then becomes
\[ \dfrac{\alpha}{\sqrt{6\pi}} [ 0+0+0 ] = 0 \label{10.24a.18}\]
which leads to the true statement
\[ 0 = 0 \]
therefore, \(\psi_2\) and \(\psi_3\) are orthogonal.
Q10.24b
a=α
Show the functions Ψ1=(4a3/π)1/4xe-a(x^2)/2 (|1>) and Ψ2=(a/4π)1/4(2ax2-1)e-a(x^2)/2are orthonormal.
S10.24b
Normal: (inf=infinity sign)
∫-infinfΨ1*Ψ1dx=(4a3/π)1/2 ∫-infinf e-a(x^2)=(4a3/π)1/2[1/2a(π/a)1/2]=1
∫-infinfΨ2*Ψ2dx=((a/4π)1/2∫-infinf(2ax2-1)e-a(x^2)=1
Orthogonal:
∫-infinfΨ1*Ψ2dx=<1|2>=(a/π1/2)∫-infinf(2ax2-1)e-a(x^2)=0
Q10.24c
Check the normalization of \(\psi_1\)and \(\psi_2\) for the harmonic oscillator and show they are orthogonal.
S10.24c
\[\psi_1=(\dfrac{4\alpha^3}{\pi})^{1/4} (x)e^{(-\alpha x^2)/{2}}\]
\[\psi_2=(\dfrac{\alpha}{4\pi})^{1/4} (2\alpha x^2 -1)e^{(-\alpha x^2)/{2}}\]
Normalization for \(\psi_1\) :
Since the function is all real, we can square it:
\[\langle \psi_1 | \psi_1 \rangle =\int ((\dfrac{4\alpha^3}{\pi})^{1/4} (x)e^{(-\alpha x^2)/{2}})^2 dx\]
\[\langle \psi_1 | \psi_1 \rangle = (\dfrac{4\alpha^3}{\pi})^{1/2} \int (x)^2e^{(-\alpha x^2)} dx\]
\[\langle \psi_1 | \psi_1 \rangle = (\dfrac{4\alpha^3}{\pi})^{1/2} \times \dfrac{1}{2 \alpha} (\dfrac{\pi}{\alpha})^{1/2} \]
After simplification we get:
\[\langle \psi_1 | \psi_1 \rangle = 1 \]
Normalization for \(\psi_2\) :
This function also does not have a complex part
There:
\[\langle \psi_2 | \psi_2 \rangle =\int ((\dfrac{\alpha}{4\pi})^{1/4} (2 \alpha x^2-1)e^{(-\alpha x^2)/{2}})^2 dx\]
\[\langle \psi_2 | \psi_2 \rangle = (\dfrac{\alpha}{4\pi})^{1/2} \int 4 \alpha x^4+1-4\alpha x^2)e^{(-\alpha x^2)} dx\]
\[\langle \psi_2 | \psi_2 \rangle = (\dfrac{\alpha}{4\pi})^{1/2} ( \int (4 \alpha^2 x^4 e^{(-\alpha x^2)} dx + \int e^{(-\alpha x^2)} dx- \int (4 \alpha x^2 e^{(-\alpha x^2)} dx)\]
\[\langle \psi_2 | \psi_2 \rangle = (\dfrac{\alpha}{4\pi})^{1/2} ( \dfrac{3\pi^{1/2}}{\alpha^{1/2}}+ \dfrac{\pi^{1/2}}{\alpha^{1/2}}-\dfrac{2\pi^{1/2}}{\alpha^{1/2}})\]
\[\langle \psi_2 | \psi_2 \rangle =1\]
Now, checking their orthogonality:
\[\langle \psi_1 | \psi_2 \rangle = \int (\dfrac{4\alpha^3}{\pi})^{1/4} (x)e^{(-\alpha x^2)/{2}} \times (\dfrac{\alpha}{4\pi})^{1/4} (2\alpha x^2 -1)e^{(-\alpha x^2)/{2}} dx\]
\[\langle \psi_1 | \psi_2 \rangle = (\dfrac{4\alpha^3}{\pi})^{1/4}\times(\dfrac{\alpha}{4\pi})^{1/4} \int (x)e^{(-\alpha x^2)} \times (2\alpha x^2 -1) dx\]
The integral is odd.Then, the value is 0 based on its symmetry.
\[\langle \psi_1 | \psi_2 \rangle = 0\]
Q10.24d
Check the normalization of \(\psi_{2}\) and \(\psi_{3}\) for harmonic oscillator and show that they are orthogonal
S10.24d
\[\psi_{2} = \left(\dfrac{\alpha}{4\pi}\right)^{\dfrac{1}{4}}(2\alpha x^2-1)e^{-\dfrac{\alpha x^2}{2}}\]
\[\psi_{3} = \left(\dfrac{\alpha^3}{9\pi}\right)^{\dfrac{1}{4}}(2\alpha x^3-x)e^{-\dfrac{\alpha x^2}{2}}\]
Normalizations:
\[\text{For }\psi_{2}\text{ : }\]
\[\int_{-\infty}^{\infty} \left(\left(\dfrac{\alpha}{4\pi}\right)^{\dfrac{1}{4}}(2\alpha x^2-1)e^{-\dfrac{\alpha x^2}{2}}\right)^2 dx\]
\[\int_{-\infty}^{\infty} \left(\dfrac{\alpha}{4\pi}\right)^{\dfrac{1}{2}}(2\alpha x^2-1)^2e^{-\alpha x^2} dx\]
\[ \left(\dfrac{\alpha}{4\pi}\right)^{\dfrac{1}{2}} \int_{-\infty}^{\infty} (4\alpha^2 x^4-2\alpha x^2 + 1) e^{-\alpha x^2} dx\]
\[ \left(\dfrac{\alpha}{4\pi}\right)^{\dfrac{1}{2}} 2\left(\sqrt{\dfrac{\pi}{\alpha}}\right)\]
\[=1\]
\[\text{For }\psi_{3}\text{ : }\]
\[\int_{-\infty}^{\infty} \left(\left(\dfrac{\alpha^3}{9\pi}\right)^{\dfrac{1}{4}}(2\alpha x^3-x)e^{-\dfrac{\alpha x^2}{2}}\right)^2 dx\]
\[\int_{-\infty}^{\infty} \left(\dfrac{\alpha^3}{9\pi}\right)^{\dfrac{1}{2}}(2\alpha x^3-x)^2e^{-\alpha x^2} dx\]
\[\left(\dfrac{\alpha^3}{9\pi}\right)^{\dfrac{1}{2}}\int_{-\infty}^{\infty} (2\alpha x^3-x)^2e^{-\alpha x^2} dx\]
\[\left(\dfrac{\alpha^3}{9\pi}\right)^{\dfrac{1}{2}} 3\left(\sqrt{\dfrac{\pi}{\alpha^3}}\right) \]
\[=1\]
Orthogonal:
\[\int_{-\infty}^{\infty} \left(\dfrac{\alpha}{4\pi}\right)^{\dfrac{1}{4}}(2\alpha x^2-1)e^{-\dfrac{\alpha x^2}{2}} \left(\dfrac{\alpha^3}{9\pi}\right)^{\dfrac{1}{4}}(2\alpha x^3-x)e^{-\dfrac{\alpha x^2}{2}} dx\]
\[\int_{-\infty}^{\infty} \left(\dfrac{\alpha}{4\pi}\dfrac{\alpha^3}{9\pi}\right)^{\dfrac{1}{4}}(2\alpha x^2-1) (2\alpha x^3-x) e^{-\alpha x^2} dx\]
\[\left(\dfrac{\alpha^4}{36\pi^2}\right)^{\dfrac{1}{4}} \int_{-\infty}^{\infty} (2\alpha x^2-1) (2\alpha x^3-x) e^{-\alpha x^2} dx\]
\[\left(\dfrac{\alpha^4}{36\pi^2}\right)^{\dfrac{1}{4}} \left(0\right)\]
\[=0\]
Q10.24e
Illustrate the harmonic oscillator functions (\(\psi_2\)) and (\(\psi_3\)) are each normal and orthogonal to each other
S10.24e
\[\psi_2=(\dfrac{\alpha}{4\pi})^{1/4} (2\alpha x^2 -1)e^{(-\alpha x^2)/{2}}\]
\[\langle \psi_2 | \psi_2 \rangle=\sqrt{\dfrac{\alpha}{4\pi}}\int_{-\infty}^\infty (2\alpha x^2-1)^2 e^{-\alpha x^2} dx\]
\[\sqrt{\dfrac{\alpha}{4\pi}}\int_{-\infty}^\infty (4\alpha^{2}x^{4}-4\alpha x^{2}+1)e^{-\alpha x^2} dx\]
\[\sqrt{\dfrac{\alpha}{4\pi}}(4\alpha^{2}\int_{-\infty}^\infty x^{4}e^{-\alpha x^2} dx -4\alpha \int_{-\infty}^\infty x^{2}e^{-\alpha x^2} dx+\int_{-\infty}^\infty e^{-\alpha x^2} dx)\]
\[\sqrt{\dfrac{\alpha}{4\pi}}(4\alpha^{2}\dfrac{3}{4\alpha^2}\sqrt{\dfrac{\pi}{\alpha}}-4\alpha \dfrac{1}{2\alpha}\sqrt{\dfrac{\pi}{\alpha}}+\sqrt{\dfrac{\pi}{\alpha}})\]
\[\sqrt{\dfrac{\alpha}{4\pi}}(3-2+1)\sqrt{\dfrac{\pi}{\alpha}}\]
\[\langle \psi_2 | \psi_2 \rangle=1\]
\[\psi_3=(\dfrac{\alpha^3}{9\pi})^{1/4} (2\alpha x^3 -3x)e^{(-\alpha x^2)/{2}}\]
\[\langle \psi_3 | \psi_3 \rangle=\sqrt{\dfrac{\alpha^3}{9\pi}}\int_{-\infty}^\infty (2\alpha x^3-3x)^2 e^{-\alpha x^2} dx\]
\[\sqrt{\dfrac{\alpha^3}{9\pi}}\int_{-\infty}^\infty (4\alpha^{2}x^{6}-12\alpha x^{4}+9x^2)e^{-\alpha x^2} dx\]
\[\sqrt{\dfrac{\alpha^3}{9\pi}}(4\alpha^{2}\int_{-\infty}^\infty x^{6}e^{-\alpha x^2} dx -12\alpha \int_{-\infty}^\infty x^{4}e^{-\alpha x^2} dx+9\int_{-\infty}^\infty x^{2}e^{-\alpha x^2} dx)\]
\[\sqrt{\dfrac{\alpha^3}{9\pi}}(4\alpha^{2}\dfrac{15}{8\alpha^3}\sqrt{\dfrac{\pi}{\alpha}}-12\alpha \dfrac{3}{4\alpha^2}\sqrt{\dfrac{\pi}{\alpha}}+9\dfrac{1}{2\alpha}\sqrt{\dfrac{\pi}{\alpha}})\]
\[\sqrt{\dfrac{\alpha^3}{9\pi}}(\dfrac{15}{2\alpha}-\dfrac{9}{\alpha}+\dfrac{9}{2\alpha})\sqrt{\dfrac{\pi}{\alpha}}\]
\[\langle \psi_3 | \psi_3 \rangle=1\]
\[\langle \psi_3 | \psi_2 \rangle=\int_{-\infty}^\infty (\dfrac{\alpha^3}{9\pi})^{1/4}(2\alpha x^{3}-x)e^{(-\alpha x^{2})/2}(\dfrac{\alpha}{4\pi})^{1/4}(2\alpha x^{2}-1)e^{(-\alpha x^{2})/2} dx\]
\[(\dfrac{\alpha^{3}}{9\pi})^{1/4}(\dfrac{\alpha}{4\pi})^{1/4}\int_{-\infty}^\infty (4\alpha^{2}x^{5}-4\alpha x^{3}+1)e^{-\alpha x^2} dx\]
since the polynomial in the integrand is an odd function the integral is equal to 0
\[(\dfrac{\alpha}{9\pi})^{1/4}(\dfrac{\alpha}{4\pi})^{1/4}(0)\]
\[\langle \psi_3 | \psi_2 \rangle=0\]
Q10.24f
Check the normalization of $$\psi_0 and \psi_1$$ for the harmonic oscillator and show they are orthogonal.
S10.24f
\[ \psi_0 = \dfrac{\alpha}{\pi}^{1/4}e^{ \dfrac{- \alpha x^2}{2}} \]
\[ \psi_1 = \dfrac{4 \alpha}{\pi}^{1/4}xe^{ \dfrac{- \alpha x^2}{2}} \]
\[ < \psi_0 | \psi_1 > = 1 \]
\[ < \psi_0 | \psi_1 > = \int^\infty_{-\infty} \dfrac{\alpha}{\pi}^{1/4}e^{ \dfrac{- \alpha x^2}{2}}\dfrac{4 \alpha}{\pi}^{1/4}xe^{ \dfrac{- \alpha x^2}{2}} \,dx \]
\[ = \dfrac{4 \alpha^4}{\pi^2}^{1/4} \int^\infty_{-\infty} xe^{- \alpha x^2} \,dx \]
\[ = \dfrac{4 \alpha^4}{\pi^2}^{1/4}0 \]
\[Since: \int^\infty_{-\infty} xe^{- \alpha x^2} \,dx = 0 \]
Q10.25a
Substitute ν = 2 eigenfunction for the harmonic oscillator into the Schrodinger equation for the harmonic oscillator and obtain the expression for the eigenvalue (energy).
S10.25a
Energy eigenvalues for harmonic oscillator (ν)
\[E_{HO} = h\omega ( \dfrac{1}{2} + \nu)\]
Energy eigenvalue for \(ν = 2\) is
\[E_{HO} = h\omega ( \dfrac{1}{2} + \nu) = h\omega ( \dfrac{1}{2} + 2) = h\omega (\dfrac{5}{2})\]
Q10.25b
Find an expression for the energy of the ground state harmonic oscillator using the Schrodinger equation.
S10.25b
The Schrodinger equation is:
\[\hat{H}\psi=E\psi\]
\(\hat{H}\) for the Harmonic Oscillator is,
\[\hat{H_{HO}}=\dfrac{-\bar{h}}{2m}\dfrac{d^2}{dx^2}+\dfrac{m\omega^2}{2}x^2\]
The ground state wave function is
\[\psi_0=(\dfrac{\alpha}{\pi})^{1/4}e^{(-\alpha x^2/2)}\]
In order to use the Schrodinger equation, we must evaluate the second derivative of \(\psi_0\).
\[\dfrac{d\psi}{dx}=-(\dfrac{\alpha}{\pi})^{1/4}\alpha x e^{(-\alpha x^2/2)}\]
\[\dfrac{d^2\psi}{dx^2}=(\dfrac{\alpha}{\pi})^{1/4}\alpha^2 x^2 e^{(-\alpha x^2/2)} - (\dfrac{\alpha}{\pi})^{1/4}\alpha e^{(-\alpha x^2/2)}=(\alpha^2 x^2 - \alpha)\psi_0\]
Substituting this into the Schrodinger equation,
\[\dfrac{-\bar{h}}{2m}(\alpha^2 x^2 - \alpha)\psi_0+\dfrac{m\omega^2}{2}x^2\psi_0=E\psi_0\]
In order for this to be a solution to the Schrodinger equation for all possible x values, the coefficients of each power of x must equal each other. Therefore,
\[-\dfrac{\bar{h^2}\alpha^2}{2m}=\dfrac{m\omega^2}{2}\]
Solving for \(\alpha\),
\[\alpha=\dfrac{m\omega}{\bar{h}}\]
Now, setting the constant terms equal yields the energy,
\[-\dfrac{\bar{h^2}\alpha^2}{2m}\dfrac{m\omega}{\bar{h}}=E_0=\dfrac{\bar{h}\omega}{2}\]
Q10.25c
Substitute the \(n=2\) eigenfunction for the harmonic oscillator into the Schrodinger Equation, and obtain the expression for the eigenvalue (energy).
S10.25c
The n=1 harmonic oscillator eigenfunction is \[ \left(\dfrac{\alpha}{4\pi}\right)^{\dfrac{1}{4}}xe^{\dfrac{\alpha x^2}{2}} \]
Which we will call \(\psi_2\) The Schrodinger equation becomes \[ \hat{H} | \psi_2\rangle= E_{HO} | \psi_2\rangle\]
by the formula sheet we know \[ E_n =\left (n+\dfrac{1}{2}\right) \hbar\omega\] so \[E_2=\left(\dfrac{3}{2}\right)\hbar\omega\]
Q10.25d
Substitute the \(v = 3\) eigenfunction for the harmonic oscillator into the schrodinger equation for the harmonic oscillator, and obtain the expression for the eigenvalue(energy). The hamiltonian for the harmonic oscillator
S10.25d
\[\hat{H} = \dfrac{\hbar^2}{2\mu} \dfrac{\partial^2}{\partial x^2}+ \dfrac{kx^2}{2}\]
The schrodinger equation is :
\[\hat{H}\psi_{v} = E_{v}\psi_{v}\label{5}\]
where E is
\[E_v=(v + \dfrac{1}{2})\hbar\omega\label{6}\]
for v = 1
\[E_{3} = (3+ \dfrac{1}{2})\hbar\omega = \dfrac{7}{2}\hbar\omega\]
Q10.25e
Substitute the v=2 eigenfunction for the harmonic oscillator into the Schrodinger equation for the harmonic oscillator, and obtain the expression for the eigenvalue (energy).
S10.25e
E= ћω [(1/2) + v]
v=2
E= ћω [(1/2) + 2] = (5/2) ћω
Q10.26a
In the vibrational motion of HI, the iodine atom essentially remains stationary because of its large mass. Assuming that the hydrogen atom undergoes harmonic motion and that the force constant k is 400 N/m , what is the fundamental vibration frequency? what is fundamental vibration frequency if H is replaced by D?
Q10.26b
In the vibrational motion of HBr, the Bromine atom essentially remains stationary because of its large mass. Assuming that the hydrogen atom undergoes harmonic motion and that the force constant k is 400 Nm-1, what is the fundamental vibration frequency v0? What is v0 if H is replaced by Tritium?
S10.26b
\[v_0=\dfrac{1}{2π} \sqrt{\dfrac{k}{m}}\]
We know the mass of a proton from the previous problem, so
\[v_0=\dfrac{1}{2π} \sqrt{\dfrac{400 Nm^{-1}}{1.67×10^{-27} kg}}=7.79×10^{13} s^{-1}\]
If Hydrogen is replaced by Tritium
\[m_T=5.01 × 10^{-27} kg\]
\[v_0=\dfrac{1}{2π} \sqrt{\dfrac{400 Nm^{-1}}{5.01×10^{-27} kg}}=4.50×10^{13} s^{-1}\]
Q10.27a
Show that
\[\begin{vmatrix} x& 1 & 0 & 0 \\ 1& x & 1 & 0\\ 0& 1& x& 1\\ 0& 0& 1& x \end{vmatrix} = 0\]
given the algebraic equation
\[\ x^4-3x^2+1=0\]
S10.27a
We expand 4 x 4 determinant and expanding along the first row gives this:
\[\\x\begin{vmatrix} x& 1 & 0 \\ 1& x & 1 \\ 0& 1& x\\ \end{vmatrix} -\begin{vmatrix} 1& 1 & 0 \\ 0& x & 1 \\ 0& 1& x\\ \end{vmatrix} =0\]
Expanding the first 3x3 determinant will give us :
\[\\x^2\begin{vmatrix} x& 1 \\ 1& x \\ \end{vmatrix} -x\begin{vmatrix} 1& 1 \\ 0& x \\ \end{vmatrix} -\begin{vmatrix} x& 1 \\ 1& x \\ \end{vmatrix}=0\]
and expanding the above 2 x 2 determinant gives :
\[\\x^2(x^2-1)-x(x)-(x^2-1)=0 \\ \\ (x^2-1)(x^2-1)-x^2 =0\\\\x^4-3x^2+1=0\]
Q10.27b
What are the expectation values for:
- momentum in the \(v=0\) state?
- square of momentum for a harmonic oscillator in the \(v=0\) state?
- What is the standard deviation for momentum in the \(v=0\) state?
S10.27b
Expectation values are the values for observables or measurable characteristics of a particle. They are found by operating on the wave function, which is the probability distribution specific for the state of the particle.
(a) Step1: Find the wave function which describes the state of the particle. For a harmonic oscillator with v=0:
\[\Psi_0(x)=(\dfrac{\alpha}{\pi})^{\dfrac{1}{4}}e^\dfrac{-\alpha x^2}{2}\]
Step 2: Find the correct operator:
\[\hat{p_x}=-i\hbar\dfrac{d}{dx}\]
Step 3: Operate on the wave function:
\[-i\hslash\dfrac{d}{dx}(\dfrac{\alpha}{\pi})^{\dfrac{1}{4}}e^\dfrac{-\alpha x^2}{2}\]
Step 4: Find the average by integrating over all space:
\[\int^\infty_{-\infty} ((\dfrac{\alpha}{\pi})^{\dfrac{1}{4}}e^\dfrac{-\alpha x^2}{2})(-i\hslash\dfrac{d}{dx}(\dfrac{\alpha}{\pi})^{\dfrac{1}{4}}e^\dfrac{-\alpha x^2}{2})\, dx\]
(b) Starting from Step 2, the operator is two applications of the momentum operator or:
\[\hat{p_x}^{2}=-\hbar^{2}\dfrac{d^{2}}{dx^{2}}\]
Step 3: Operate on the wavefunction:
\[-\hbar^{2}\dfrac{d^{2}}{dx^{2}}(\dfrac{\alpha}{\pi})^{\dfrac{1}{4}}e^\dfrac{-\alpha x^2}{2}\]
\[\int^\infty_{-\infty} ((\dfrac{\alpha}{\pi})^{\dfrac{1}{4}}e^\dfrac{-\alpha x^2}{2})([-\hbar^{2}\dfrac{d^{2}}{dx^{2}}(\dfrac{\alpha}{\pi})^{\dfrac{1}{4}}e^\dfrac{-\alpha x^2}{2})\, dx\]
\[\left<\hat{p_x}^2\right>=\dfrac{1}{2}\hbar^{2}\alpha\] Given that \[\int^\infty_{-\infty} e^{-\alpha x^2}\, dx = \sqrt{\dfrac{\pi}{\alpha}}\] \[\int^\infty_{-\infty} x^{2n}e^{-\alpha x^2}\, dx = \sqrt{\dfrac{\pi}{\alpha}}\dfrac{1*3*5...(2n-1)}{2^{n}a^{n}}\]
(c) The standard deviation is given by:
\[\sqrt {\left<\hat{p_x}^{2}\right>-{\left<\hat{p_x}\right>}^{2}}\]
Which equals
\[\hbar\sqrt{\dfrac{\alpha}{2}}\]
Q10.27c
What are the expectation value \(\langle x\rangle\) and \(\langle x^2 \rangle\) for a quantum mechanical oscillator in the v=0 state. What is the standard deviation ?
S10.27c
For v=0 state the wavefuntion is \(\Psi_0 (x)\)
\[\langle x \rangle = \int_{-\infty}^\infty \psi_0^*(x) \hat{x}\ \psi_0(x) dx\]
\[\langle x \rangle = \int_{-\infty}^\infty (\dfrac{\alpha}{\pi})^{\dfrac{1}{4}} e^{\dfrac{-\alpha x^2}{2}} (x) (\dfrac{\alpha}{\pi})^{\dfrac{1}{4}} e^{\dfrac{-\alpha x^2}{2}} dx\]
\[\langle x \rangle = (\dfrac{\alpha}{\pi})^{\dfrac{1}{2}} \int_{0}^\infty xe^{-\alpha x^2} dx\]
\[\langle x \rangle= \dfrac {1}{2\alpha}\]
Then we take the expectation value of \(\langle x^{2} \rangle\) :
\[\langle x^2 \rangle = \int_{-\infty}^\infty \psi_0^*(x) \hat{x^2}\ \psi_0(x) dx\]
\[\langle x^2 \rangle = \int_{-\infty}^\infty (\dfrac{\alpha}{\pi})^{\dfrac{1}{4}} e^{\dfrac{-\alpha x^2}{2}} (x^2) (\dfrac{\alpha}{\pi})^{\dfrac{1}{4}} e^{\dfrac{-\alpha x^2}{2}} dx\]
\[\langle x^2 \rangle = (\dfrac{\alpha}{\pi})^{\dfrac{1}{2}} \int_{0}^\infty x^2e^{-\alpha x^2} dx\]
\[\langle x^2 \rangle= (\dfrac{1}{4\alpha}) \sqrt{\dfrac{\pi}{\alpha}}\]
After obtaining both \(\langle x\rangle\) and \(\langle x^{2} \rangle\) we can use the results to get the Standard deviation \Delta x.
\[ \Delta x= \sqrt{\langle x^2\rangle -\angle x\rangle ^2}\]
\[\Delta x=\sqrt{(\dfrac{\pi^{\dfrac{1}{2}}}{4\alpha^{\dfrac{3}{2}}}) - (\dfrac{1}{4\alpha^{2}})}\]
Q10.27d
What are the expectation values for \(\langle p_x \rangle\) and \( \langle p_x^2 \rangle\) for a quantum mechanical harmonic oscillator in the \(v=0\) state? What is the standard deviation \(\Delta p_x\)?
S10.27d
The ground state harmonic oscillator is given by
\[\psi_0 (x) = (\tfrac{\alpha}{\pi})^{1/4} e^{\tfrac{-\alpha x^2}{2}}\]
Solving for the expectation value of momentum
\[\langle p_x \rangle = \langle \psi_0|p_x|\psi_0\rangle = \langle \psi_0|-i\hbar\tfrac{d}{dx}|\psi_0\rangle\]
Moving out constants we have
\[\langle p_x \rangle = -i\hbar(\tfrac{\alpha}{\pi})^{1/2} \langle \psi_0|\tfrac{d}{dx}|\psi_0\rangle\]
Differentiate and move out constants
\[\langle p_x \rangle = i\alpha\hbar(\tfrac{\alpha}{\pi})^{1/2} \langle \psi_0|x|\psi_0\rangle\]
Solving the integral
\[\langle p_x \rangle = i\alpha\hbar(\tfrac{\alpha}{\pi})^{1/2} \int_{-\infty}^{\infty}xe^{-\tfrac{\alpha x^2}{2}}dx\]
The Gaussian integral equates to zero
\[\langle p_x \rangle = 0\]
Now repeat for \(\langle p_x^2 \rangle\)
\[\langle p_x^2 \rangle = \langle \psi_0|p_x^2|\psi_0\rangle = \langle \psi_0|(-i\hbar\tfrac{d}{dx})^2|\psi_0\rangle\]
Differentiate twice (careful, second derivative involves the chain rule) and pull out constants
\[\langle p_x^2 \rangle = -\alpha\hbar^2(\tfrac{\alpha}{\pi})^{1/2}( \langle \psi_o | \psi_0 \rangle -\alpha \langle \psi_0|x^2|\psi_0 \rangle)\]
Since the wave functions are normalized, the first integral is 1. The second is another Gaussian
\[\langle p_x^2 \rangle = -\alpha\hbar^2((\tfrac{\alpha}{\pi})^{1/2}- 1/2)\]
Now that we have \(\langle p_x \rangle\) and \( \langle p_x^2 \rangle\), we can solve for \(\Delta p_x^2\)
\[\Delta p_x^2 = -\langle p_x^2 \rangle - (\langle p_x \rangle)^2 = \alpha\hbar^2((\tfrac{\alpha}{\pi})^{1/2}- 1/2) - 0\]
Finally, solve for \(\Delta p_x\) by taking the square root of the previous expression
\[\Delta p_x = -\alpha^{1/2}\hbar \sqrt{(\tfrac{\alpha}{\pi})^{1/2}-1/2}\]
Q10.28a
What are the reduced mass and moment of inertia of \(\ce{^23Na^{79}Br }\)? The equilibrium internuclear distance \(R_e\) is 250 pm. What are the values of \(E\) for the states with \(J=1\) and \(J= 2\).
S10.28a
The mass of \(\ce{^{23}Na}\) is \(m_1 = 22.99 u\) and \(\ce{^{79}Br}\) is \(m_2 = 78.92 u\). The reduced mass is defined as the product of the two masses divided by the sum of the two masses.
\[\mu = \dfrac{m_1 \cdot m_2}{m_1 + m_2} = \dfrac{(22.99 u) (78.92 u)}{22.99 u + 78.92 u} (1.661 \times 10^{-27} kg/u)= 2.957 \times 10^{-26} kg\]
The moment of inertia is defined as a product of the mass (reduced mass in this instance) and distance squared.
\[I=\mu {R_e}^2 = (2.957 \times 10^{-26} kg) (250 \times 10^{-12} m)^2 = 1.848 \times 10^{-45} \; kg \times m^2 \]
Using the rigid rotator as a model for our rotating diatomic molecule, the energy is then
\[E_J = \dfrac{{\hbar}^2 J \cdot (J+1)}{2 I}\label{4}\]
Using equation \((4)\) the values of \(E\) for the states with \(J=1\) and \(J= 2\) can be calculated.
\[E_1 = \dfrac{(1.055 \times 10^{-34} \; J \; s)^2 \;1 \cdot (1+1)}{2 \; (1.848 \times 10^{-45} \; kg \; m^2)} = 6.022 \times 10^{-24} \; J\]
\[E_2 = \dfrac{(1.055 \times 10^{-34} \; J \; s)^2 \;2 \cdot (2+1)}{2 \; (1.848 \times 10^{-45} \; kg \; m^2)} = 1.807 \times 10^{-23} \; J\]
Q10.28b
- What are the reduced mass and moment of inertia of \(\ce{^{39}K^{79}Br}\) if the internuclear distance is R (meters)? Note: keep answer in terms of R for part (a).
- What type of EM radiation is emitted in the transition from \(J=2\) to \(J=3\) if \(R=250pm\)?
S10.28b
(a):
The reduced mass is given by: \[\mu =\dfrac{m_{K}m_{Br}}{m_{K}+m_{Br}}\]\[=\tfrac{(6.470075\cdot 10^{-26})(1.3104697\cdot 10^{-25})}{(6.470075\cdot 10^{-26})+(1.3104697\cdot 10^{-25})}=4.33151\cdot 10^{-26}kg\]
Moment of inertia: \[I=\mu \cdot r^{2}\] where r is the internuclear distance (R in this problem):
\[I=(4.33151\cdot 10^{-26}kg)R^{2}\]
(b):
The energy associated with J is given by:
\[E_{J}=\dfrac{J(J+1)\hbar^{2}}{2I}\]
For the transition from 2 to 3:
\[\Delta E_{2\rightarrow 3}=\dfrac{\hbar^{2}}{2I}[3(3+1)-2(2+1)]=\dfrac{3\hbar^{2}}{I}\]
\[\Delta E_{2\rightarrow 3}=\dfrac{\hbar^{2}}{6.926\cdot 10^{-25}R^{2}}=2.569\cdot 10^{-25}J\]
But \(E=h\cdot f\) , so:
\[f_{2\rightarrow 3}=\dfrac{\Delta E_{2\rightarrow 3}}{h}=287.7MHz\]
which is a frequency associated with micro and radio waves
Q10.29b
show that :"\[[\hat{L_y},\hat{L_z}]=i\hslash\hat{L_x}\]
Use the following relationships and properties of commutators:
\[\hat{L_x}=y\hat{P_z}-z\hat{P_y}\]
\[\hat{L_z}=x\hat{P_y}-y\hat{P_x}\]
\[\hat{L_y}=z\hat{P_x}-x\hat{P_z}\]
S10.29b
\[[\hat{L_y},\hat{L_z}]=[z\hat{P_x}-x\hat{P_z},x\hat{P_y}-y\hat{P_x}]\]
\[[\hat{L_y},\hat{L_z}]=[z\hat{P_x},x\hat{P_y}]-[z\hat{P_x},y\hat{P_x}]-[x\hat{P_z},x\hat{P_y}]+[x\hat{P_z},y\hat{P_x}]\]
By using the properties of commutators, we get:
\[[z\hat{P_x},x\hat{P_y}]=z[\hat{P_x},x]\hat{P_y}=-i\hslash\hat{P_y}z\]
\[[z\hat{P_x},y\hat{P_x}]=z[\hat{P_x},\hat{P_x}]y=0\]
\[[x\hat{P_z},x\hat{P_y}]=\hat{P_z}[\hat{x},\hat{x}]\hat{P_y}=0\]
\[[x\hat{P_z},y\hat{P_x}]=\hat{P_z}[x,\hat{P_x}]y=i\hslash\hat{P_z}y\]
Therefore, \[[\hat{L_y},\hat{L_z}]=-i\hslash\hat{P_y}z+i\hslash\hat{P_z}y=i\hslash[\hat{P_z}y-z\hat{P_y}]=i\hslash\hat{L_x}\]
Q10.29c
The commutator of two operators,
\[\hat{A}, \hat{B}\]
is defined as the operator
\[\hat{A}\hat{B}-\hat{B}\hat{A}.\]
Using the definitions of \[\hat{L_x},\hat{L_y},\hat{L_z},\]
find\[ [\hat{L_x},\hat{L_y}] \]
and
\[ [\hat{L_y},\hat{L_z}] .\]
S10.29c
\[ \hat{L_x} = y\hat{P_z} - z\hat{P_y} \]
\[ \hat{L_y} = y\hat{P_x} - z\hat{P_z} \]
\[ \hat{L_z} = y\hat{P_y} - z\hat{P_x} \]
\[ [\hat{L_y},\hat{L_z}] = [z\hat{P_x}-x\hat{P_z}, x\hat{P_y}-y\hat{P_x}] \]
Using the commutator relationship
\[ [A+B, C+D] = [A,C] + [A,D] + [B,C] + [B,D] \]
\[ [\hat{L_y} \hat{L_z}] = [z\hat{P_x}, x\hat{P_y}] - [z\hat{P_x}, y\hat{P_x}] - [x\hat{P_z}, x\hat{P_y}] - [x\hat{P_z}, y\hat{P_x}] \]
\[ [z\hat{P_x}, x\hat{P_y}] = z\hat{P_x}x\hat{P_y} - x\hat{P_y}z\hat{P_x} = z\hat{P_y}(\hat{P_x}x) - z\hat{P_y}(x\hat{P_x}) = z\hat{P_y}[\hat{P_x},x] \]
\[ [\hat{P_x},x]f = (\hat{P_x}x-x\hat{P_x})f \]
\[ = -i \hbar \dfrac{\partial}{\partial x} (xf) + i \hbar x \dfrac{\partial f}{\partial x} = i \hbar [-f - x\dfrac{\partial f}{\partial x} + x\dfrac{\partial f}{\partial x} ] \]
\[ [\hat{P_x},x]f = -i\hbar f \]
\[ \implies [\hat{P_x},x] = i\hbar (*) \]
\[ \implies [z\hat{P_x},x\hat{P_y}] = z\hat{P_y}(-i\hbar) \]
\[ [z\hat{P_x}, y\hat{P_x} ] = z\hat{P_x}y\hat{P_x} - y\hat{P_x}z\hat{P_x} = zy(\hat{P_x}\hat{P_x} - \hat{P_x}\hat{P_x}) = 0 \]
\[ [x\hat{P_z}, x\hat{P_y}] = x\hat{P_z}x\hat{P_y} - x\hat{P_y}x\hat{P_z} = x^2(\hat{P_z}\hat{P_y} - \hat{P_y}\hat{P_z}) = 0 \]
\[ [x\hat{P_z}, y\hat{P_x}] = x\hat{P_z}y\hat{P_x} - y\hat{P_x}x\hat{P_z} = y\hat{P_z}(x\hat{P_x}-\hat{P_x}x) = y\hat{P_z}[x,\hat{P_x}] \]
\[ [x, \hat{P_x}]f = (x\hat{P_x} - \hat{P_x}x)f = x(-i \hbar \dfrac{\partial f}{\partial x}) + i \hbar \dfrac{\partial}{\partial x}(xf) = i \hbar (-x \dfrac{\partial f}{\partial x} + f + x\dfrac{\partial f}{\partial x}) \]
\[ [x, \hat{P_x}]f = i \hbar f \]
\[ [x, \hat{P_x}] = i \hbar (* *) \]
Therefore,
\[ [\hat{L_y}, \hat{L_z}] = z\hat{P_y}(-i \hbar) - 0 - 0 + y\hat{P_z}(i \hbar) = i \hbar (y\hat{P_z} - z\hat{P_y} ) = i \hbar \hat{L_x} \]
\[ [\hat{L_z}, \hat{L_x}] = [x\hat{P_y}-y\hat{P_x}, y\hat{P_z}-z\hat{P_y}] = [x\hat{P_y}, y\hat{P_z}] - [x\hat{P_y},z\hat{P_y}] - [y\hat{P_x}, y\hat{P_z}] = [y\hat{P_x},z\hat{P_y}] \]
\[ [x\hat{P_y}, y\hat{P_z}] = x\hat{P_y}y\hat{P_z} - y\hat{P_z}x\hat{P_y} = x\hat{P_z}(\hat{P_y}y - y\hat{P_y}) = x\hat{P_z}[\hat{P_y},y] \]
As shown in *,
\[ [\hat{P_y},y] = -i \hbar \]
\[ [x\hat{P_y}, y\hat{P_z}] = x\hat{P_z}(-i \hbar) \]
\[ [x\hat{P_y}, z\hat{P_y}] = x\hat{P_y}z\hat{P_y} - z\hat{P_y}x\hat{P_y} = xz(\hat{P_y}\hat{P_y} - \hat{P_y}\hat{P_y}) = 0 \]
\[ [y\hat{P_x}, y\hat{P_z}] = y\hat{P_x}y\hat{P_z} - y\hat{P_z}y\hat{P_x} = y^2(\hat{P_x}\hat{P_z} - \hat{P_z}\hat{P_x}) = 0 \]
\[ [y\hat{P_x}, z\hat{P_y}] = y\hat{P_x}z\hat{P_y} - z\hat{P_y}y\hat{P_x} = z\hat{P_x}(y\hat{P_y} - \hat{P_y}y) = z\hat{P_x}[y,\hat{P_y}] \]
As shown in (**),
\[ [y,\hat{P_y}] = i \hbar \]
\[ [y\hat{P_x}-z\hat{P_y}] = z\hat{P_x}(i \hbar) \]
Therefore,
\[ [\hat{L_z},\hat{L_x}] = x\hat{P_z}(-i \hbar) - 0 - 0 + z\hat{P_x}(i \hbar) = i \hbar (-x\hat{P_z} + z\hat{P_x}) = i \hbar (z\hat{P_x} - x\hat{P_z}) = i \hbar \hat{L_y} \]
Q10.29d
Given the following:
\[[L{_x},L{_y}]=i\hbar L_z\]
\[[L{_x},L{_z}]=-i\hbar L_y\]
\[[L{_x},L{_x}]=0\]
Show that:
\[[L{_x},L^{2}]=0\]
S10.29d
If we expand \(L^2\) we get:
\[L^{2}=L{_{x}^{2}}+L{_{y}^{2}}+L{_{z}^{2}}\]
The new equation that we are trying to solve is now:
\[[L{_x},L{_{x}^{2}}+L{_{y}^{2}}+L{_{z}^{2}}]=[L{_x},L{_{x}^{2}}]+[L{_x},L{_{y}^{2}}]+[L{_z},L{_{x}^{2}}] (eq.1)\]
From the given information we see that the first term from eq.1 is zero :
\[[L{_x},L{_{x}^{2}}]=0\]
The other two terms can be easily calculated using the given information and the properties of commutators as follows:
\[[L{_x},L{_{y}^{2}}]=[L{_x},L{_{y}}]L{_y}+L{_y}[L{_x},L{_{y}}]=2i \hbar(L{_z}L{_y})\]
\[[L{_x},L{_{z}^{2}}]=[L{_x},L{_{z}}]L{_z}+L{_z}[L{_x},L{_{z}}]=-2i \hbar(L{_y}L{_z})\]
Putting all the pieces from above together we get:
\[[L{_x},L{_{x}^{2}}+L{_{y}^{2}}+L{_{z}^{2}}]=0+2i\hbar(L{_z}L{_y})-2i\hbar(L{_y}L{_z})=0\]
Q10.30a
The molecule 14N16O has an equilibrium bond distance of 115 pm.
(14N, 14.00674 amu ; 16O, 15.9994 amu)
Calculate (a) the reduced mass and (b) the moment of inertia.
(c) Calculate the wavelength of the photon emitted when the molecule makes the transition from l =1 to l = 0. For the energy levels, use equation:
\[E_l = \dfrac{\hbar^2}{2I} l(l+1)\]
S10.30a
(a) $$\mu=\dfrac{m1\cdot m2}{m1+m2}\]
Use the formula to get the reduced mass. (Don't forget: The given masses of 14N and 16O are in amu, so divide by Avogadro's number.)
\[=\dfrac{14.00674\times15.9994}{14.00674+15.9994}\times\dfrac{1}{6.022\times10^{23}}\]
\[=1.24019\times10^{-23}g=1.24019\times10^{-26}kg\]
(b)$$I=\mu r^2=1.24019\times10^{-26}\times(115\times10^{-12})^2\]
\[=1.6402\times10^{-46}kg\cdot m^2\]
(c) $$E_l = \dfrac{\hbar^2}{2I} l(l+1)\]
\[\Delta E= E_0-E_1=\dfrac{\hbar^2}{2I} 0(0+1)-\dfrac{\hbar^2}{2I} 1(1+1)\]
We take the positive answer because it asks for the wavelength emitted by the photon.
\[|\Delta E|= \dfrac{\hbar^2}{I}=\dfrac{hc}{\lambda}\]
Rearranging the equation:
\[\lambda=\dfrac{hcI}{\hbar^2}\]
\[\hbar=\dfrac{h}{2\pi}\]
\[\lambda=\dfrac{4\pi^2 cI}{h}\]
\[=\dfrac{4\pi^2\times2.998\times10^8\times1.6402\times10^{-46}}{6.626\times10^{-34}}\]
\[=2.9298\times10^{-3}m\]
Q10.30b
The 12C16O molecule has an equilibrium bond distance of 112.8 pm. Calculate (a) the reduced mass and (b) the moment of inertia. (c) Calculate the wavelength of the photon emitted when the molecule makes the transition from l = 2 to l = 1.
S10.30b
a) Carbon-12 has a mass of 12 amu and Oxygen-16 has a mass of 16 amu, so using the reduced mass formula
\[ \mu = \dfrac{m_1 m_2}{m_1 + m_2}\]
the reduced mass is 48/7 amu, or 1.139e-26 kg.
b) The moment of inertia is calculated using the bond distance and reduced mass in the formula
\[ \textit{I} = \mu r^2 = 1.139\times 10^{-26} kg * (112.8\times 10^{-12} m)^2 = 1.449\times 10^{-46}kg*m^2 \]
c) This molecule can be modeled as a rigid rotor. To find the wavelength of the emitted photon, we must first determine the energy of the photon using the energy levels of the rigid rotor
\[ E = \dfrac{\hbar^2 l(l+1)}{2I} \]
where we want to find \(\Delta E = E_{l=1} - E_{l=2}\).
\[ E_{l=1} = \dfrac{(1.055 \times 10^{-34})^2 * 2}{2 * 1.449\times 10^{-46}} = 7.682 \times 10^{-23} J \]
\[ E_{l=2} = \dfrac{(1.055 \times 10^{-34})^2 * 6}{2*1.449 \times 10^{-46}} = 2.305 \times 10^{-22} J \]
So the magnitude of the energy released, which is the energy of the photon, is \(E = 1.536\times 10^{-22}\)
It is trivial to find the wavelength using \(E = \dfrac{h c}{\lambda}\)
\[\lambda = 1.29 mm\]
Q10.30
The following molecule has an equilibrium bond distance of 112.8pm.
\[^{12}C^{16}O\]
- Calculate the reduced mass of the molecule
- Calculate the moment of inertia
- Calculate the change in rotational energy from the state l=0 to l=1
S10.30
a.
\[\mu = \dfrac{m_1+m_2}{m_1m_2}\]
\[\mu = \dfrac{m_C+m_O}{m_Cm_O}\]
\[\mu = \dfrac{1.996x10^{-26}kg+2.657x10^{-26}kg}{1.996x10^{-26}2.657x10^{-26}kg}\]
\[= 8.774x10^{26}kg\]
b.
\[I = \mu r^{2}\]
\[=8.774x10^{-26}kg 1.128x10^{-10}m\]
\[=9.897x10^{-36}kgm\]
c.
\[E_{rotation} = \dfrac{L^{2}}{2I}\]
\[L^{2}=l(l+1)\hbar\]
\[E_{rotation} = \dfrac{l(l+1)\hbar}{2I}\]
\[\Delta E_{rotation} = \dfrac{\hbar}{1.9794x10^{-35}kgm}\]
QS9.40
Does quantum mechanics agree with classical mechanics regarding energy density, \(\rho(v,T)\) when h → 0?
S9.40
Classical equation: \[\rho_{classical} = \dfrac{8\pi v^2}{c^3}kT\]
Quantum Equation: \[\rho_{quantum} = \dfrac{8\pi h (v/c)^3}{e^{hv/kT}-1}\]
as h approaches 0, \[\rho_{quantum}= \dfrac{8\pi v^3}{c^3}\dfrac{kT}{v} = \dfrac{8\pi v^2}{c^3}kT = \rho_{classical}\]
However this is a fundamentally flawed assumption to be made. At high frequencies the classical assumption approaches infinity while the quantum mechanical model has a bell curve that approaches 0 at high frequencies. This is the 'Ultra-violet' catastrophe.
Q9.42
(a) Using the result of Problem 9.41, find the maximum emission frequency at 3000 K and at 10 000 K. (b) Using the Wien displacement law, equation 9.186, find the maximum emission wavelength at the same two temperatures.
S9.42
From the Planck distribution law,
\[\rho_\nu = \dfrac{8\pi h (v/c)^3}{e^{\dfrac {h\nu}{k_B T}} - 1}\]
\[\rho_\nu (\nu,T) = \dfrac{8\pi h \nu^{3}}{c^{3}} \dfrac{1}{e^{\dfrac {h\nu}{k_B T}} - 1}\]
h = 6.626 x 10-34 Js
c = 3.00 x 108 m/s
kB = 1.38 x 10-23 J/K
(a) By differentiating \(\rho_\nu (\nu,T)\) with respect to T, we find
\[0 = \dfrac{8\pi h^{2} \nu^{4} e^{\dfrac{h\nu}{k_B T}}}{c^{3} k_B T^{2} (e^{\dfrac{h\nu}{k_B T}} - 1)^{2}}\]
\[\nu_{max} = (T)(1.035 \times 10^{11} \space \dfrac{1}{s K})\]
At 3000 K,
\[\nu_{max} = (3000 \space K)(1.035 \times 10^{11} \space \dfrac{1}{s K}) = 3.106 \times 10^{14} \space s^{-1}\]
At 10000 K,
\[\nu_{max} = (10000 \space K)(1.035 \times 10^{11} \space \dfrac{1}{s K}) = 1.035 \times 10^{15} \space s^{-1}\]
(b) The Wien displacement law is \[\lambda_{max} T = 2.898 \times 10^{-3} \space K m\]
\[\lambda_{max} = \dfrac{2.898 \times 10^{-3} \space K m}{T}\]
At 3000 K,
\[\lambda_{max} = \dfrac{(2.898 \times 10^{-3} \space K m)}{(3000 \space K)} = 9.66 \times 10^{-7} \space m\]
At 10000 K,
\[\lambda_{max} = \dfrac{(2.898 \times 10^{-3} \space K m)}{(10000 \space K)} = 2.898 \times 10^{-7} \space m\]
Q9.43
Calculate the de Broglie wavelength (a) of an electron accelerated by a potential of 1000 V and (b) of a proton accelerated by a potential of 1000 V.
S9.43
\[eV = \dfrac{1}{2}mv^2\]
\[v = \sqrt{\dfrac{2eV}{m}}\]
\[λ = \dfrac{h}{mv}\]
(a) Mass of an electron: 9.11 x 10-31 kg
\[v = \sqrt{\dfrac{(2)(1.6 \times 10^{-19} \space C)(1000 \space V)}{9.11 \times 10^{-31} \space kg}} = 18741994.3 \space m/s\]
\[λ = \dfrac{6.626 \times 10^{-34} \space Js}{(9.11 \times 10^{-31} \space kg)(18741994.3 \space m/s)} = 3.88 \times 10^{-11} \space m\]
(b) Mass of a proton: 1.67 x 10-27 kg
\[v = \sqrt{\dfrac{(2)(1.6 \times 10^{-19} \space C)(1000 \space V)}{1.67 \times 10^{-27} \space kg}} = 437740.524 \space m/s\]
\[λ = \dfrac{6.626 \times 10^{-34} \space Js}{(1.67 \times 10^{-27} \space kg)(437740.524 \space m/s)} = 9.06 \times 10^{-13} \space m\]
Q10.51a
What is the reduced mass of 16O2 ? What is the moment of inertia if given Re = 120.7 pm. Find the energies of the first three levels of rotational motion.
S10.51a
Reduced Mass:
\[µ = \dfrac{m_1m_2}{m_1+m_2} \]
\[ µ = \dfrac{16*16}{16+16} = \dfrac{256}{32} = 8 \]
Moment of Inertia:
\[ I = MR^2_e = 8 * (120.7)^2 = 1.166 \times 10^5 \]
Rotational Motion:
\[ E_{rot} = \dfrac{J\left(J + 1\right)\hbar^2}{2MR^2_e} \]
\[ At J = 0 , \dfrac{\hbar^2}{2MR^2_e} \]
\[ At J = 1 , \dfrac{2\hbar^2}{2MR^2_e} \]
\[ At J = 2 , \dfrac{6\hbar^2}{2MR^2_e} \]
Q10.51b
What is the reduced mass of 22Na34Cl? What is its moment of inertia if Re = 236pm? Find the energy of the first two levels of rotational motion.
S10.51b
We know the mass of a sodium atom is 22.990 amu and the mass of a chlorine atom is 35.4527 amu. The conversion factor we need to use is 1.6605e10-27 kg/amu. This will make our answer in terms of kilograms, rather than atomic mass units. The reduced mass equation is:
\[\mu=\dfrac{\mu_{Na}\mu_{Cl}}{\mu_{Na}+\mu_{Cl}}\]
Plug in the values you have for each mass:
\[\mu=\dfrac{(22.990amu)(35.4527amu)}{(22.990amu)+(35.4527amu)}\]
\[\mu=\dfrac{815.0576amu^2}{58.4427amu}\]\[\mu=13.9462amu\]
To express this value in terms of kilograms, multiply by the conversion factor:
\[\mu=(13.9462amu)(1.6605e10^{-27}\dfrac{kg}{amu})\]\[\mu=2.3157e10^{-26}kg\]
Now to find the moment of inertia. In order to do this, we use the equation: \[I=(\mu)(R^2)\]Plugging in our values for µ and R:
\[I=(2.3157e10^{-26}kg)(236pm)\]\[I=5.4652e10^{-24}kg•amu\]
In order to calculate the energy of the first two levels of rotational motion, use the equation:
\[E=\dfrac{J(J+1)h^2}{2I}\]
With J representing the level of rotation and h=1.055e10-34J•s. Plug in these values for the first and second level of rotational motion.
\[E(1)=\dfrac{1(1+1)(1.055e10^{-34})^2}{2(5.4652e10^{-24})}\]
\[E(1)=\dfrac{2.226e10^{-68}}{1.0930e10^{-23}}\]\[E(1)=2.0366e10^{-45} J\]
\[E(2)=\dfrac{2(2+1)(1.055e10^{-34})^2}{2(5.4652e10^{-24})}\]
\[E(2)=\dfrac{6.33e10^{-68}}{1.0930e10^{-23}}\]\[E(2)=5.7914e10^{-45} J\]
Q10.51c
What is the reduced mass of \(\ce{^1H^{35}Cl }\) ? What is its moment of inertia if \(R_e =127\; pm \). Using equation (5.45) Find the energies of the first three levels of rotational motion.
\[E= \dfrac{l(l+1)\hbar^2}{2I}\ \label{5.45}\]
S10.51c
To find the reduced mass of any diatomic element, use the formula \[u= \dfrac{m_1m_2}{m_1+m_2}\] where m_1 is the molar mass of the first element (times amu which is \(1.66 \times 10^{-27} \) ) and m_2 is the molar mass of the second element (times amu), in this case \(m_1 = 1.0078 amu = 1.673 \times 10^{-27}\) and \(m_2 = 34.9688 amu = 5.805 \times 10^{-26}\). Now
\[u= \dfrac{(1.673 \times 10^{-27})(5.805 \times 10^{-26})}{1.673 \times 10^{-27}+5.805 \times 10^{-26}}\]
\[u=1.627 \times 10^{-27}\]
Now to find the moment of inertia, use this formula \[I= uR^2_e\].
Do not forget to convert \(R_e\) to metric units (meters) now \(R_e = 127 \times 10^{-12}\; m \)
\[I = (1.627 \times 10^{-27})(127 \times 10^{-12})^2 = 2.623 \times 10^{-47}\]
Finally, plug I into equation 5.45, where l is the energy state (the first three energy states are l=0,1,2) \(\hbar \) is just a constant \(\hbar = 1.055 \times 10^{-34}\; m^2 kg /s \)
- The answer for l = 0 is \(0 \)
- The answer for l = 1 is \(4.2438 \times 10^{-22} \)
- The answer for l = 2 is \(1.2731 \times 10^{-21} \)