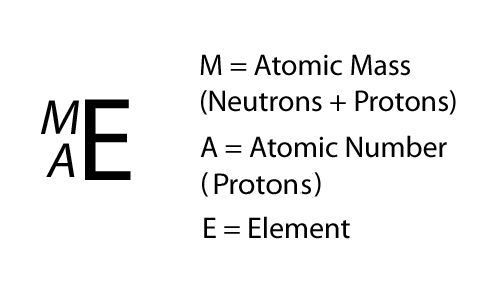
Atomic MassTable of contents
The mass of an atom or a molecule is often called its atomic mass. Mass is a basic physical property of matter and striclty speaking there is no difference between mass and atomic mass. Therefore the term 'atomic mass 'is really technobabble. The (atomic) mass is used to find the average mass of elements and molecules and to help solve stoichiometry problems.
IntroductionIn chemistry, there are many different concepts of mass that are often used incoherently and are often ill defined. It is often assumed that atomic mass is the mass of an atom indicated in unified atomic mass units (u). However, the book "Quantities, Units and Symbols in Physical Chemistry" published by the IUPAC clearly states: Neither the name of the physical quantity, nor the symbol used to denote it, should imply a particular choice of unit.
The name "atomic mass" is a historical baggage and comes from the fact that chemistry was the first science that investigated the same physical objects on macroscopic and microscopic levels. In addition the situation is rendered more complicated by the isotopic distribution. On the macroscopic level, most mass measurements of pure substances refer to a mixture of isotopes. This means from a physical stand point, these mixtures are not pure. For example, the macroscopic mass of oxigen (O2) does not correspond to the microscopic mass of O2. The former usually implies a certain isotopic distribution, whereas the later usually refes to the most common isotope (16O2). Note that the former is now often referred to as the "molecular weight" or "atomic weight".
In the following the different concepts are explained. Average MassIsotopes are atoms with the same atomic number, but different mass number. The larger mass size is due to the difference in the number of nuetrons that an atom contains. Although mass numbers are whole numbers, the actual masses of individual atoms are never whole numbers (except for carbon-12). This explains how Lithium can have an atomic mass of 6.941 Da. The atomic masses on the periodic table take these isotopes into account, weighing them based on their abundance in nature, therefore, more weight is given to the isotopes that occur most frequently in nature. Average mass of the element E is defined as: m(E) = ∑(m(In)*p(In)) where ∑ represents a n-times sumation over all isotopes In of element E, and p(I) represents the relative abundance of the isotope I.
Find the average atomic mass of boron using the Table 1 below: Mass and abundance of Boron isotopes
Solution: The average mass of Boron is: m(B) = (10.013 Da)(.199) + (11.009 Da)(.801) = 1.99 Da + 8.82 Da = 10.81 Da Relative MassTraditionally it was common practice in chemistry to not use any units when indicating atomic masses (e.g. masses on microscopic scale). Even today you can overhear chemsitry jargon like "12C has exactly mass 12". However, since mass is not a dimensionless quantity, it is clear that a mass indication in fact needs a unit. Since chemists are very sticky when it comes to jargon, many of them tried to rationalize why they don't need a unit instead of using a unit. The result is the concept of relative mass, which strictly speaking is not even a mass but a ratio of two masses. Rather than using a unit, these sticky chemists claim to indicate the ratio of the mass they want to indicate and the atomic mass constant mu which is defined analoguous to the unit they want to avoid. Hence the relative atomic mass of the mass m is defined as: Ar = m / mu It is now dimensionless and does not have any units. This trick is highly confusing and against the standards of modern metrology. Therefore we recommend not to use any "relative" mass. Molecular Weight, Atomic Weight, Weight vs. MassIn former times the concept of mass was not clearly distinguished by the concept of weight. In colloquial language this is still the case. Many people indicate their "weight" when they actually mean their mass. Mass is a fundamental property of objects, wehreas weight is a force. Weight is the force F exerted on a mass m by a gravitational field. The exact definition of the weight is controversial. Weight is an outdated concept and should no longer be used. The weight of a person is different on ground than on a plane. Stricly speaking, the weight even changes with your location on earth. When talking about atoms and molecules, it is obvious that people address the mass of a molecule when they say "molecular weight". Unfortunately, many chemists prefer their outdated jargon over scientific rigour. There is not even an agreed definition of the term "molecular weight". However, the majority of the chemists agree that it means an average mass, and many think it is dimensionless. This would make "molecular weight" a synonym to "average relative mass". Integer Mass Since the proton and the neutron have simillar mass, and the electron has a very small mass compared to the former, most molecules have a mass that is close to an integer value when measured in daltons. Therefore it is quite common to only indicate the integer mass of molecules. Integer mass is only meaningful when using the unit dalton (or u). Accurate MassMany mass spectrometers can detirmine the mass of molecules more accuratley than to the integer mass. These measurements are then called accurate mass of the molecule. The reason isotopes and hence molecules have atomic masses that are not integer masses is because of mass defect caused by binding energy in the nucleus. Units The atomic mass is usually measured in the units unified atomic mass unit (u), or dalton (Da). Both units are derived from the carbon-12 isotope, as 12 u is the exact atomic mass of that isotope. So 1 u is 1/12 of the mass of a carbon-12 isotope: 1 u = 1 Da = m(12C)/12 It is expected that the somewhat clumbsy "unified atomic mass unit" will soon be replaced by the more modern dalton. The first scientists to measure atomic mass were John Dalton (between 1803 and 1805) Jons Jacoband Berzelius (between 1808 and 1826). Early atomic mass theory was purposed by the English chemist William Prout in a series of published papers in 1815 and 1816. Known was Prout's Law, Prout propsed that the known elements all had atomic weights that were whole number multiples of the atomic mass of hydrogen. Berzelius discovered that this was not always true by showing that chlorine (Cl) had a mass of 35.45 which was not a whole number multiple of hydrogen's mass. Note that some people use the atomic mass unit (amu). The amu had two definitions. It was defined differently by physicists and by chemists. Physics: 1 amu = m(16O)/16 Chemistry: 1 amu = m(O)/16 This means the chemists used Oxigen in the naturally occurring isotopic distribution as the reference. Since the isotopic distribution in nature can change, this definition is a moving target. Therefore both communities agreed to the compromise of using m(12C)/12 as the new unit, and they called this unit "unified atomic mass unit" u. Hence, the amu is no longer in use and the people that still use it probably use it with the definition of the u in mind. Again we have a very confusing situation. This is why the use of the unit dalton (Da) is more and more recommended, whose definition is clear and whose name is not as clumbsy. Historical note: Why did one compromise on m(12C)/12 instead of the already established well defined m(16O)/16? The reason are the sticky chemsists (see above) that refused to use units. All their papers and books were written without mass units. Therefore a change of unit was a desaster for those books: you could not tell wether the amu or the u was used. The sollution was to use m(12C)/12 as the new unit which is very close to chemists amu = m(O)/16. The physicists could live with that because they usually used units in their publications, hence there was no ambigouity. Take-home message: do use units. Another note: Both, the u and the Da are not SI units. However, they are recognized by the SI. Molar MassThe molar mass is the mass of one mole of substance, whether the substance is an element or a compound. A mole of substance is equal to Avogadro's number or 6.023x10^23 atoms. The molar mass is indicated in the units g/mol or kg/mol. When using the unit g/mol, the numerical value of the molar mass of a molecule is the same as its average mass in dalton: Average mass of C: 12.011 Da Molar mass of C: 12.011 g/mol This allows for a smooth transition from the microsopic world, where mass is measured in dalton, to the macroscopic world where mass is measured in kg.
What is the molar mass of phenol, C6H5OH? Average mass m = 6 * 12.011 Da + 6 * 1.008 Da + 1 * 15.999 Da = 94.113 Da Molar mass = 94.113 g/mol = 0.094113 kg/mol Measuring Masses in the Atomic ScaleMasses of atoms and molecules are measured by a mass spectrometer. Mass Spectrometry is a technology to measure the mass-to-charge ratio m/Q of ions. This implies that all molecules and atoms to be measured must first be ionized. After this, the ions are then seperated in a mass analyzer according to their mass-to-charge ratio. The charge of the measured ion can then usually be figured out because it is a multiple of the elementary charge. Then the ion's mass can be deduced. The average masses indicated in the Periodic Table are then calculated using the isotopic abundances, as explained above. Note that the masses of all isotopes have been measured with very high accuracy. Therefore it is much simpler and more accurate to calculate the mass of a molecule as a sum of its isotopes than measuring it with a commercial mass spectrometer. Note that the same is not true on the nucleon scale. The mass of an isotope cannot be calculated accurately as the sum of its particles (table below) since this would ignore the mass defect caused by the binding energy of the nucleons, which is significant.
As one can see in Table 2, the mass of an electron is relatively small so that it only contributes less than 1/1000 to the overall mass of the atom. Where to Find Atomic MassThe atomic mass found on the Periodic Table (below the element's name) is the average atomic mass. For example, for Lithium:
The red arrow indicates the atomic mass of Lithium. As shown in Table 2 above and mathematically explained later, the masses of a protons and neutrons are about 1u. This, however, does not explain why Lithium has an atomic mass of 6.941 Da were we would expect 6 Da. You can notice this for all elements on the Periodic Table. The atomic mass for Lithium is actually the average atomic mass based on its Isotopes. We will go into further details on this on the next section. One particularly useful way of writing an isotope is as follows: AZE
E = Element A = Mass Number Z = Atomic number = Proton Number N = A - Z = Number of Neutron Number ApplicationsApplications Include:
*Please Note: One particularly important relationship is illustrated by the fact that an atomic mass unit is equal to 1.66 * 10-24 g. This is the reciprocal of Avogadro's constant, but this is no mere coincidence: \[ \displaytype \dfrac{\rm Atomic~Mass~(g)}{1 {\rm g}} \times \dfrac{1 {\rm mol}}{6.022 \times 10^{23}} = \dfrac{\rm Mass~(g)}{1 {\rm atom}}\] Because a Mol can also be expressed as gram x atoms, 1u = Mu(molar mass unit)/NA(Avogadro's Number)=1g/mol/NA NA known as Avoagrado's Number or Constant is equal to 6.023x10^23 atoms. Atomic mass is particularly vital when dealing with Stoichiometry. StoichiometryStoichiometry includes quantitative relationships among reactants, products, and the chemical interactions between them.
How many moles of CO2 are produced in the combustion of 2.27 mol of triethylene glycol, C6H14O4, in an excess of O2? First, write the chemical reaction: 2 C6H14O4 + 5 O2 --> 4 CO2 + 6 H2O Notice that 4 mol CO2 are produced for every 2 mol C6H14O4. (2.72 mol C6H14O4) x (4 mol CO2 / 2 mol C6H14O4) = 5.44 mol CO2 Practice Problemsa) What is the molecular mass of Radium Bicarbonate, or Ra(HCO3)2? b) List the following, from least to greatest, in terms of their number of neutrons, and then atomic mass: 14N, 42Cl, 25Na, 10Be c) A new element Zenium, has 3 isotopes, 59Ze, 61Ze, and 67Ze, with abundances of 62%, 27%, and 11% respectively. What is the atomic mass of Zenium? d) An isotope with a mass number of 55 has 5 more neutrons than protons. What element is it? e) How much mass does 3.71 moles of Fluorine have? f) How many grams are there in 4.3 x 1022 molecules of POCl3? g) How many moles are there in 23 grams of sodium carbonate? Solutions a) Molecular mass of Ra(HCO3)2 = 226 + 2(1.01 u + 12.01 u + (16.00 u)(3)) = 348 u or g/mol b) Number of neutrons: 10Be, 14N, 25Na, 42Cl Atomic Mass: 10Be, 14N, 25Na, 42Cl Note: It is the same increasing order for both number of neutrons and atomic mass because more neutrons means more mass. c) Atomic mass of Zenium: (59 u)(0.62) + (61 u)(0.27) + (67 u)(0.11) = 37 u + 16 u + 7.4 u = 60.4 u or g/mol d) Mn e) (3.71 moles F2)(19 x 2 g/mol F2) = (3.71 mol F2)(38 g/mol F2) = 140 g F2 f) (4.3 x 1022 molecules POCI3)(1 mol/6.022 x 1023 molecules POCI3)(30.97 + 16.00 + 35.45 x 3 g/mol POCI3) = (4.3 x 1022 molecules POCI3)(mol/6.022 x 1023 molecules POCI3)(153.32 g/mol POCI3) = 11 g POCI3 g) (23 g Na2CO3)(1 mol/22.99 x 2 + 12.01 + 16.00 x 3 g Na2CO3) = (23 g Na2CO3)(1 mol/105.99 g Na2CO3) = (.22 mol Na2CO3) Outside LinksReferences
Contributors
This page viewed 63825 times
 UC Davis ChemWiki by University of California, Davis is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License. TweetPermissions beyond the scope of this license may be available at copyright@ucdavis.edu. Terms of Use Powered by Mindtouch Core 2010
You must login to post a comment.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.png)
