5.9B: Reaction Mechanisms
- Page ID
- 1417
Reaction mechanisms are step-by-step descriptions of what occurs on a molecular level in chemical reactions. Each step of the reaction mechanism is known as an elementary process, a term used to describe a moment in the reaction when one or more molecules changes geometry or is perturbed by the addition or omission of another interacting molecule. Collectively, an overall reaction and a reaction mechanism consist of multiple elementary processes. These elementary steps are the basic building blocks of a complex reaction, and cannot be broken down any further. Because a reaction mechanism is used to describe what occurs at each step of a reaction, it also describes the transition state, or the state in which the maximum of potential energy is reached. A mechanism must show the order in which the bonds form or break and the rate of each elementary step. Also accounted for are the reaction intermediates, stable molecules that do not appear in the experimentally determined rate law because they are formed in one step and consumed in a subsequent step.
A mechanism must satisfy the following two requirements:
- The elementary steps must add up to give the overall balanced equation for the reaction.
- The rate law for the rate-determining step must agree with the experimentally determined rate law.
Each of these events constitutes an elementary step that can be represented as a coming-together of discrete particles ("collision") or as the breaking-up of a molecule ("dissociation") into simpler units. The molecular entity that emerges from each step may be a final product of the reaction, or it might be an intermediate.
Elementary Processes
Although a rate law for an overall reaction can only be experimentally determined, the rate law for each elementary step can be deduced from the chemical equation through inspection. A unimolecular elementary step has a first order rate law, whereas a bimolecular elementary step has a second order rate law. Table \(\PageIndex{1}\) summarizes the types of elementary steps and the rate laws that they follow. \(A\), \(B\), and \(C\) here represent the reactants or reaction intermediates. Typically these steps are usually either unimolecular or bimolecular. A unimolecular elementary process describes the dissociation of a single molecule. A bimolecular elementary process occurs when two molecules collide. A third process, called termolecular, is rare because it involves three molecules colliding at the same time. In the bimolecular andtermolecular processes, the molecules may be different or the same.
| Molecularity | Elementary Step | Rate Law for Elementary step |
|---|---|---|
| Unimolecular | \[A \longrightarrow products\] | \[\text{rate}= k[A]\] |
| Bimolecular | \[A + B \longrightarrow products\] | \[\text{rate}= k[A][B]\] |
| \[A + A \longrightarrow products\] | \[\text{rate}= k[A]^2\] | |
| Termolecular | \[A + A + B \longrightarrow products\] | \[\text{rate}= k[A]^2[B]\] |
| \[A + A + A \longrightarrow products\] | \[\text{rate} = k[A]^3\] | |
| \[A + B + C \longrightarrow products\] | \[\text{rate}= k[A][B][C]\] |
Elementary processes are also reversible. Some may reach conditions of equilibrium, in which both the forward and reverse reaction rates are equal.
Bimolecular Elementary Processes
Example \(\PageIndex{4}\): Mechanism with a slow step followed by a fast step
Consider the reaction between the gases iodine monochloride and hydrogen produce two gases, iodine and hydrogen chloride as products.
\[\ce{H2(g) + 2 ICl (g) -> I_2 (g) + 2 HCl (g)} \nonumber\]
Through experiment, the rate law is found to be,
\[\text{rate of reaction} = k [\ce{H2}] [\ce{ICl}]\nonumber\]
Using a proposed reaction mechanism:
\[H_2+ ICl \overset{k_1}{\longrightarrow} HI + HCl \tag{step 1}\]
\[HI + ICl \overset{k_2}{\longrightarrow} I_2 + HCl \tag{step 2}\]
with \( k_2 >> k_1\). The corresponding rate laws for each elementary step are
\[ \dfrac{[HI]}{dt} = \dfrac{[HCl]}{dt} = k_1 [H_2] [ICl] \tag{step 1}\]
\[ \dfrac{[I_2]}{dt} = \dfrac{[HCl]}{dt} = - \dfrac{[HI]}{dt} = -\dfrac{[ICI]}{dt} = k_2 [HI] [ICl] \tag{step2}\]
The mechanism chosen for the reaction above proposes that Step 1 is the rate-determining step, because it occurs more slowly. According to the proposed mechanism, the rate law agrees that the mechanism works for this reaction. The rate of Step 1 = K1 [H2] [ICl] is in agreement with the experimentally determined rate law, so the mechanism matches the stoichiometry of the overall reaction. However, this does not mean that the mechanism is correct. It only shows that the chosen mechanism works perfectly for this reaction. This is a reasonable proposal.
When there is enough energy for the slow reaction to occur, the reaction moves to a faster step, Step 2, which occurs rapidly. The mechanism suggests that HI is consumed in the second step as quickly as it is formed. \(HI\) is, therefore, the reaction intermediate.
The diagram below shows the reaction progress of the two-step mechanism proposed. Notice that the reaction intermediate and the transition states are short-lived, but the intermediate can be isolated due to its fully formed bonds.
Diagram of a Two-Step Reaction

Example \(\PageIndex{6}\) : Mechanism with a fast step followed by slow step
Below is the equation of nitric oxide reacting with oxygen to produce nitrogen dioxide:
\[\ce{2 NO (g) + O_2 \longrightarrow 2 NO_2 (g)} \nonumber\]
which has an experimentally determined third order rate law:
\[\text{rate of reaction} = k [\ce{NO_2}]^2[\ce{O_2}] \nonumber\]
Because a termolecular mechanism (a three-body reaction occurring in a single step) is extremely rare, a mechanism with two bimolecular elementary steps can be suggested:
\[ 2 NO (g) \rightleftharpoons N_2O_2 (g) \tag{Step 1 fast}\]
\[N_2O_2 (g) + O_2 (g) \longrightarrow 2 NO_2 (g) \tag{Step 2 slow}\]
The proposed mechanism has the same stoichiometry as the overall reaction. Step 1 is a reversible process in which equilibrium is reached quickly. Step 2 is therefore the rate-determining step. The relative rate of the Step 2 is \(k_3[N_2O_2][O_2]\), which does not seem to match with the experimental rate of \(k [NO_2]^2[O_2]\). However, N2O2 is actually a reaction intermediate, because it appears in both elementary steps but not in the equation of the overall reaction. Because an intermediate cannot appear in the rate law for the overall reaction, a value equivalent to \(\ce{N2O2}\) is required. Because Step 1 is a fast, reversible reaction, it can be assumed that:
\[k_1 [NO]^2 = k_2 [N_2O_2] \nonumber\]
Therefore,
\[[N_2O_2] = \dfrac{k_1}{k_2} [NO]^2 \nonumber\]
Through substitution,
\[k_3[N_2O_2][O_2] = k_3 \left(\dfrac{k_1}{k_2}\right) [NO]^2[O_2] \nonumber\]
The rate constant is \(k = k_3 \dfrac{k_1}{k_2}\), so the rate of reaction is \(k [NO]^2[O_2]\), matching the experimental rate law. This proposed mechanism fulfills both requirements for a possible mechanism.
The Steady-State Approximation
In some reaction mechanisms, more than one elementary step may control the rate of the reaction. In such mechanisms, no assumptions about the rates of the steps within the mechanism can be made. For example, take the reaction of nitric oxide (\(NO\)) with molecular oxygen (\(O_2\)):
\[2NO + O_2 \longrightarrow 2NO_2\]
As discussed in the example above, the mechanism for this reaction involves two steps:
\[NO+ NO\; \underset{k_{-1}}{\overset{k_1}{\longrightleftharpoons}} \; N_2O_2 \label{step 1}\]
\[N_2O_2 +O_2 \overset{k_2}{\longrightarrow} 2NO_2 \label{step 2}\]
To find the overall reaction rate without knowledge of the rate-determining step (if it exists) can be tricky. Let's start by selecting one of the terminal elementary steps and writing its reaction rate:
\[ \text{Reaction Rate} = k_2[N_2O_2][O_2] \label{1}\]
However, the intermediate \(N_2O_2\) from step 1 remains in this expression, so this does not represent the final rate law. To eliminate this reaction intermediate, we use the other elementary step, assuming that the \([N_2O_2]\) reaches a steady-state condition (i.e., unchanging amplitude).
\[ \dfrac{d[N_2O_2]}{dt} \approx 0 \label{2}\]
This approximation implies the rate of generation of \(N_2O_2\) from step 1 is equal to its decay in step 2. Using this assumption, the rate of formation of \([N_2O_2]\) can be written in terms of \(NO\) from step 1:
\[\text{rate of formation of } N_2O_2 = \underset{\text{step 1}}{k_1[NO]^2} \label{3}\]
The rate of disappearance of \(N_2O_2\) is separated into two parts, giving the equation:
\[ \text{rate of disappearance of } N_2O_2 = \underset{\text{step 1}}{k_{-1}[N_2O_2]} + \underset{\text{step 2}}{k_2[N_2O_2][O_2]} \label{4}\]
Equating the two equations results in:
\[k_1[NO]^2 = k_{-1}[N_2O_2] + k_2[N_2O_2][O_2] \label{5}\]
Rearranging this equation to solve for the steady state population of \([N_2O_2]\) gives
\[[N_2O_2] = \dfrac{k_1[NO]^2}{k_{-1}+k_2[O_2]} \label{6}\]
Substituting this value of \([N_2O_2]\) into Equation \ref{1} provide us with the proper rate law for this reaction predicted by the proposed two-step mechanism:
\[\text{rate} = \dfrac{k_1k_2[O_2][NO]^2}{k_{-1}+k_2[O_2]} \label{7}\]
Most overall reactions do not occur in a single step and involve mechanisms with successive elementary steps.
We can never "prove" the correct mechanism for a reaction
Reaction mechanisms can never be proven to be correct, they can shown to not predict the experimental data and hence "disproved."
Problems
- When we find a reaction mechanism, according to the rate law, that perfectly works to solve a complex reaction, why can we not say that the reaction mechanism proves that the rate law is right?
- Which elementary process is bimolecular?
(a) A\(\longrightarrow\) products
(b) A + B\(\longrightarrow\) products
(c) A + A + B\(\longrightarrow\) products
(d) Both (b) and (c) - Propose a mechanism for the reaction 2 NO(g) + O2 (g) \(\longrightarrow\) 2 NO2 (g) and show that the chosen mechanism is consistent with the rate law: k[NO]2[O2].
- For the reaction, 2NO2(g) + F2(g) \(\longrightarrow\) 2NO2F with a rate law = k[NO2][F2]:
(a) write the steps for a bimolecular elementary process.
(b) identify which elementary process is the rate determinant and which one is the fast reaction. - The decomposition of hydrogen peroxide is catalyzed by iodide ion:
2 H202 (aq)\( \xrightarrow[ ]{I^-}\) 2H2O (l) + O2 (g) Rate = k [H2O2] [I]
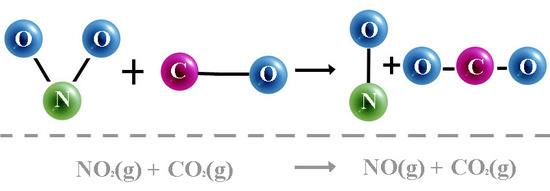
Find a possible mechanism and identify the intermediate. - NO2 (g) + CO (g)\(\longrightarrow\) NO (g) + CO2 (g)
The experimental rate = k[NO2]2
Explain why the following mechanism cannot be used. Propose a plausible mechanism and identify the rate-determining step.
Solutions
- A reaction mechanism is only a rationalization of how a reaction progresses. It cannot be proven to be true. There may be more than one possible proposed mechanism, in which the slow elementary process is considered the rate-determining step.
- (b) \( A + B \longrightarrow \text{products}\) is a bimolecular process because two molecules are involved.
- Refer back to the example under "A Mechanism with a Fast Reversible First Step Followed by a Slow Step."
- (a) Step (1): NO2 + F2\(\longrightarrow\) NO2F + F Rate (1): k1[NO2][F2]
Step (2): NO2+ F\(\longrightarrow\) NO2F Rate (2): k2[NO2][F]
_________________________________________________________________________
Overall Reaction: 2 NO2 + F2\(\longrightarrow\) 2NO2F
Step (1) and (2) add up to an overall reaction that matches the stoichiometry of the given equation. The rate of Step (2) is consistent with the experimental rate law. Therefore, the proposed mechanism works.
(b) The slowest elementary process gives the rate of the overall reaction. Because the rate of Step (2) matches the experimental rate law, Step (2) is the rate determinant. Step (1) has a faster reaction. - Step (1): H2O2 + I-\(\longrightarrow\) H2OH + IO- (Intermediate) Rate (1) = k1 [H2O2][I-]
Step (2): H2O2 +IO-\(\longrightarrow\) H2O + O2 + I- (Catalyst) Rate (2)= k2 [H2O2][IO-]
_______________________________________________________
Overall Reaction: 2 H202 (aq)\( \xrightarrow[ ]{I^-}\) 2H2O (l) + O2 (g) Rate = k [H2O2] [I]
Although I- appears in both elementary steps, it is a catalyst in the reaction, so it can occur in the rate law, unlike the intermediate, IO-. - Although the one-step mechanism proposed in this problem satisfies the molecular equation, it's rate of reaction (k [NO2][CO]) does not agree with the experimentally determined rate law.
Step (1): NO2+ NO2\(\longrightarrow\) NO3 + NO Rate (1)= k1 [NO2]2
Step (2): NO3 + CO\(\longrightarrow\) NO2 +CO2 Rate (2) = k2 [NO3][CO]
___________________________________________________
Overall Reaction: 2 NO2 + CO\(\longrightarrow\) NO + CO2
NO2 and NO3 are intermediates. Step (1) has the same rate as the experimental rate law, so it is the rate-determining step.
References
- Fábián, István. Reaction Kinetics, Mechanisms and Catalysis. Springer, 2009.
- Kinetics and Mechanism Concept Test Questions: www.jce.divched.org/JCEDLib/QBank/collection/ConcepTests/kinetics.html
- Petrucci, Ralph. General Chemistry, Principles and Modern Applications. Ninth Edition. Chemical Kinetics, Reaction Mechanism, pg 596-602.
- Kemp, T. J. Progress in Reaction Kinetics & Mechanism. Science Reviews, 2000 Ltd.
- Upadhyay, Santosh K. Chemical Kinetics and Reaction Dynamics. Springer, 2007.
- Zumdahl, Steven S. Chemistry. Fifth edition. Chemical Kinetics, Reaction Mechanism, pg 583-586.
- Petrucci, Ralph. General Chemistry, Principles and Modern Applications. Custom Edition. Chemical Kinetics, Reaction Mechanism, pg 1093-1097
Contributors and Attributions
- Abel Silva, Marisol Ahumada, RyanBricknell (UCD)

