2.5: Reaction Rate
- Page ID
- 1438
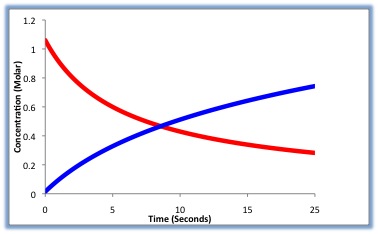
During the course of the reaction shown below, reactants A and B are consumed while the concentration of product AB increases. The reaction rate can be determined by measuring how fast the concentration of A or B decreases, or by how fast the concentration of AB increases.
\[ \ A + B \longrightarrow AB \nonumber \]
.jpg?revision=1&size=bestfit&width=378&height=234)
For the stochiometrically complicated Reaction:
\[ aA + bB \longrightarrow cC + dD \label{1} \]
\[ \text{Rate} = \dfrac{-1}{a}\dfrac{d[A]}{dt} = \dfrac{-1}{b} \dfrac{d[B]}{dt} = \dfrac{1}{c}\dfrac{d[C]}{dt} = \dfrac{1}{d}\dfrac{d[D]}{dt} \nonumber \]
Looking at Figure \(\PageIndex{1}\) above, we can see that the rate can be measured in terms of either reactant (A or B) or either product (C or D). Not all variables are needed to solve for the rate. Therefore, if you have the value for "A" as well as the value for "a" you can solve for the reaction rate.
You can also notice from Equation \ref{1} that the change in reactants over the change in time must have a negative sign in front of them. The reason for this is because the reactants are decreasing as a function of time, the rate would come out to be negative (because it is the reverse rate). Therefore, putting a negative sign in front of the variable will allow for the solution to be a positive rate.
Chemical reactions vary greatly in the speed at which they occur. Some are ultrafast, while others may take millions of years to reach equilibrium.
Definition of Reaction Rate
The Reaction Rate for a given chemical reaction is the measure of the change in concentration of the reactants or the change in concentration of the products per unit time. The speed of a chemical reaction may be defined as the change in concentration of a substance divided by the time interval during which this change is observed:
\[ \text{rate}=\dfrac{\Delta \text{concentration}}{\Delta \text{time}} \label{2-1} \]
For a reaction of the form \(A + B \rightarrow C\), the rate can be expressed in terms of the change in concentration of any of its components
\[\text{rate}=-\dfrac{\Delta [A]}{\Delta t} \nonumber \]
\[\text{rate}=-\dfrac{\Delta [B]}{\Delta t} \nonumber \]
\[\text{rate}=\dfrac{\Delta [C]}{\Delta t} \nonumber \]
in which \(Δ[A]\) is the difference between the concentration of \(A\) over the time interval \(t_2 – t_1\):
\[ \Delta [A] = [A]_2 – [A]_1 \label{2-2} \]
Notice the minus signs in the first two examples above. The concentration of a reactant always decreases with time, so \(\Delta [A]\) and \(\Delta [A]\) are both negative. Since negative rates do not make much sense, rates expressed in terms of a reactant concentration are always preceded by a minus sign to make the rate come out positive.
Consider now a reaction in which the coefficients are different:
\[A + 3B \rightarrow 2D \nonumber \]
It is clear that \([B]\) decreases three times as rapidly as \([A]\), so in order to avoid ambiguity when expressing the rate in terms of different components, it is customary to divide each change in concentration by the appropriate coefficient:
\[\text{rate}= -\dfrac{\Delta [A]}{\Delta t} = -\dfrac{\Delta [B]}{3\Delta t} = \dfrac{\Delta [D]}{2\Delta t} \label{2-3} \]
For the oxidation of ammonia
\[\ce{4 NH3 + 3O2 -> 2 N2 + 6 H2O} \nonumber \]
it was found that the rate of formation of N2 was 0.27 mol L–1 s–1.
- At what rate was water being formed?
- At what rate was ammonia being consumed?
Solution
a) From the equation stoichiometry, Δ[H2O] = 6/2 Δ[N2], so the rate of formation of H2O is
3 × (0.27 mol L–1 s–1) = 0.81 mol L–1 s–1.
b) 4 moles of NH3 are consumed for every 2 moles of N2 formed, so the rate of disappearance of ammonia is
2 × (0.27 mol L–1 s–1) = 0.54 mol L–1 s–1.
Comment: Because of the way this question is formulated, it would be acceptable to express this last value as a negative number.
Instantaneous rates
Most reactions slow down as the reactants are consumed. Consequently, the rates given by the expressions shown above tend to lose their meaning when measured over longer time intervals Δt. Note: Instantaneous rates are also known as differential rates.
Thus for the reaction whose progress is plotted here, the actual rate (as measured by the increasing concentration of product) varies continuously, being greatest at time zero. The instantaneous rate of a reaction is given by the slope of a tangent to the concentration-vs.-time curve.
An instantaneous rate taken near the beginning of the reaction (t = 0) is known as an initial rate (label (1) here). As we shall soon see, initial rates play an important role in the study of reaction kinetics. If you have studied differential calculus, you will know that these tangent slopes are derivatives whose values can very at each point on the curve, so that these instantaneous rates are really limiting rates defined as
\[ \text{rate} = \lim_{\Delta t \rightarrow 0} \dfrac{-[A]}{\Delta T} \nonumber \]
If you do not know calculus, bear in mind that the larger the time interval Δt, the smaller will be the precision of the instantaneous rate.
Rate Laws and Rate Constants
A rate law is an expression which relates that rate of a reaction to the rate constant and the concentrations of the reactants. A rate constant, \(k\), is a proportionality constant for a given reaction. The general rate law is usually expressed as:
\[ \text{Rate} = k[A]^s[B]^t \label{2} \]
As you can see from Equation \ref{2} above, the reaction rate is dependent on the concentration of the reactants as well as the rate constant. However, there are also other factors that can influence the rate of reaction. These factors include temperature and catalysts. When you are able to write a rate law equation for a certain reaction, you can determine the Reaction Order based on the values of s and t.
Reaction Order
The reaction rate for a given reaction is a crucial tool that enables us to calculate the specific order of a reaction. The order of a reaction is important in that it enables us to classify specific chemical reactions easily and efficiently. Knowledge of the reaction order quickly allows us to understand numerous factors within the reaction including the rate law, units of the rate constant, half life, and much more. Reaction order can be calculated from the rate law by adding the exponential values of the reactants in the rate law.
\[ \text{Rate} = k[A]^s[B]^t \label{4} \]
\[ \text{Reaction Order} = s + t \label{5} \]
It is important to note that although the reaction order can be determined from the rate law, there is in general, no relationship between the reaction order and the stoichiometric coefficients in the chemical equation.
NOTE: The rate of reaction must be a non-negative value. It can be zero and does not need to be an integer.
As shown in Equation \ref{5}, the complete reaction order is equal to the sum of "s" and "t." But what does each of these variables mean? Each variable represents the order of the reaction with respect to the reactant it is placed on. In this certain situation, s is the order of the reaction with respect to [A] and t is the order of the reaction with respect to [B].
Here is an example of how you can look at this: If a reaction order with respect to [A] was 2 (s = 2) and [B] was 1 (t = 1), then that basically means that the concentration of reactant A is decreasing by a factor of 2 and the concentration of [B] is decrease by a factor of 1.
So if you have a reaction order of Zero (i.e., \(s + t = 0\)), this basically means that the concentration of the reactants does not affect the rate of reaction. You could remove or add reactants to the mixture but the rate will not change.
A list of the different reaction rate equations for zero-, first-, and second-order reactions can be seen in Table \(\PageIndex{1}\). This table also includes further equations that can be determine by this equation once the order of the reaction is known (Half life, integrated rate law, etc.)
| Zero-Order | First-Order | Second-Order | |
|---|---|---|---|
| Rate Law |
\(\ {Rate} = \ {k}\) |
\(\ {Rate} = \ {k[A]}\) |
\(\text{Rate} = \ {k[A]^2}\) |
| Integrated Rate Law |
\(\ {[A]_t} = \ {-kt + [A]_0}\) |
\(\ {ln[A]_t} = \ {-kt + ln[A]_0}\) |
\(\dfrac{1}{[A]_t} = +kt + \dfrac{1}{[A]_0} \) |
| Units of Rate Constant (k): |
\(\ {mol L^{-1} s^{-1}}\) |
\(s^{-1}\) |
\(\ {L mol^{-1} s^{-1}}\) |
| Linear Plot to Determine (k): |
\( [A] \) versus time |
\(\ln [A] \) versus time |
\(\dfrac{1}{[A]}\) versus time |
| Relationship of Rate Constant to the Slope of Straight Line: |
\(\ {slope} = \ {-k}\) |
\(\ {slope} = \ {-k}\) |
\(\ {slope} = \ {k}\) |
| Half-life: |
\(\dfrac{[A]_0}{2k}\) |
\(\dfrac{\ln2}{k}\) |
\(\dfrac{1}{k[A]_0}\) |
Sample Problems
1. Define Reaction Rate
2. TRUE or FALSE: Changes in the temperature or the introduction of a catalyst will affect the rate constant of a reaction
For sample problems 3-6, use Formula 6 to answer the questions
\[ H_2O \longrightarrow 2H_2+ O_2 \label{6} \]
*Assume the reaction occurs at constant temperature
3. For the given reaction above, state the rate law.
4. State the overall order of the reaction.
5. Find the rate, given k = 1.14 x 10-2 and [H2O] = 2.04M
6. Find the half-life of the reaction.
Answers
1. Reaction Rate is the measure of the change in concentration of the disappearance of reactants or the change in concentration of the appearance of products per unit time.
2. FALSE. The rate constant is not dependant on the presence of a catalyst. Catalysts, however, can effect the total rate of a reaction.
3. \(\ {Rate} = \ {k[H_2O]}\)
4. First - Order
5. 2.33 x 10-2 s-1
6. 60.8 s ((t1/2 = ln 2 / k = ln 2 / 1.14 x 10-2 = 60.8 s).
References
- Chang, Raymond. (2005). Physical Chemistry for the Biosciences. Sausalito,CA: University Science Books.
- Crowe, Jonathan, Bradshaw, Tony, MonkPaul. (2006) Chemistry for the Biosciences: The Essential Concepts. Oxford Press.
- Isaacs, N.S. (1995). Physical Organic Chemistry (Second edition). Harlow UK: Adison Wesley Longman.
- Kenneth Connors. (1990). Chemical Kinetics. VCH Publishers.
- Levine, Ira N. (1988). Physical Chemistry (Third edition). McGraw-Hill Inc.
- Segel, Irwin. (1993). Enzyme Kinetics. Wiley Classics Library.
- Zumdahl, Steven S. and Zumdahl, Susan A. (2003) Chemistry (Sixth edition). Houghton Mifflin Co.
- Shagoury, Richard. Chemistry 1A Lecture Book. 4th Ed. Custom Publishing. 2006. Print
Contributors and Attributions
- Florence-Damilola Odufalu, Pamela Chacha, Galaxy Mudda, Andrew Iskandar (UCD)
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

