Radioactive Decay Rates
- Page ID
- 1489
Radioactive decay is the loss of elementary particles from an unstable nucleus, ultimately changing the unstable element into another more stable element. There are five types of radioactive decay: alpha emission, beta emission, positron emission, electron capture, and gamma emission. Each type of decay emits a specific particle which changes the type of product produced. The number of protons and neutrons found in the daughter nuclei (the nuclei produced from the decay) are determined by the type of decay or emission that the original element goes through.
Introduction
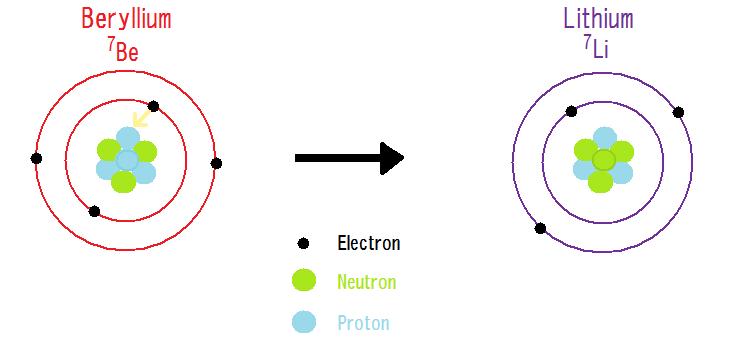
In terms of entropy, radioactive decay can be defined as the tendency for matter and energy to gain inert uniformity or stability. For elements, uniformity is produced by having an equal number of neutrons and protons which in turn dictates the desired nuclear forces to keep the nuclear particles inside the nucleus. However, any instance where one particle becomes more frequent than another creates a nucleus that becomes unstable. The unstable nucleus then releases radiation in order to gain stability. For example, the stable element Beryllium usually contains 4 protons and 5 neutrons in its nucleus (this is not considered a very large difference). However, there exists a lighter isotope of Beryllium which contains 4 protons and only 3 neutrons, which gives a total mass of 7 amu. This lighter isotope decays into Lithium-7 through electron capture. A proton from Beryllium-7 captures a single electron and becomes a neutron. This reaction produces a new isotope (Lithium-7) that has the same atomic mass unit as Beryllium-7 but one less proton which stabilizes the element.
Another example is the element Uranium-238 which has 54 more neutrons than its protons (Atomic umber =92). This element gains stability by passing through various types of decays (19 steps-- also known as the Uranium series) and is converted into Pb-206 (atomic number 82).For further information about different types of decay that Uranium goes through, refer to Decay Pathways).
Decay Rates
Due to the smaller size of the nucleus compared to the atom and the enormity of electromagnetic forces, it is impossible to predict radioactive decay. The atomic nucleus which is in the center of the atom is buffered by surrounding electrons and external conditions. Because of this, the study of decay is independent of the element's environment. In other words, the decay rate is independent of an element's physical state such as surrounding temperature and pressure. For a given element, the decay or disintegration rate is proportional to the number of atoms and the activity measured in terms of atoms per unit time. If "A" represents the disintegration rate and "N" is number of radioactive atoms, then the direct relationship between them can be shown as below:
\[ A \propto N \label{1A}\]
or mathematically speaking
\[ A= \lambda N \label{1B} \]
where
- \(A\) is the Total activity and is the number of decays per unit time of a radioactive sample.
- \(N\) is the total number of particles in the sample.
- \( \lambda \) is the constant of proportionality or decay constant.
Decay Rate & Chemical Kinetics
Since the decay rate is dependent upon the number of radioactive atoms, in terms of chemical kinetics, one can say that radioactive decay is a first order reaction process. Even though radioactive decay is a first order reaction, where the rate of the reaction depends upon the concentration of one reactant (r = k [A][B] = k [A}) , it is not affected by factors that alter a typical chemical reactions. In other words, the reaction rate does not depend upon the temperature, pressure, and other physical determinants. However, like a typical rate law equation, radioactive decay rate can be integrated to link the concentration of a reactant with time. Also, radioactive decay is an exponential decay function which means the larger the quantity of atoms, the more rapidly the element will decay. Mathematically speaking, the relationship between quantity and time for radioactive decay can be expressed in following way:
\[\dfrac{dN}{dt} = - \lambda N \label{2A}\]
or more specifically
\[\dfrac{dN(t)}{dt} = - \lambda N \label{2B}\]
or via rearranging the separable differential equation
\[\dfrac{dN(t)}{N (t)} = - \lambda dt \label{3}\]
by Integrating the equation
\[\ln N(t) = - \lambda t + C \label{4}\]
with
- \(C\) is the constant of integration
- \(N(t)\) is the amplitude of \(N\) after lapse of time \(t\)
- \(\lambda\) is the decay rate constant.
One could derive equation 4 in following manner, too. The decay rate constant, \(\lambda\), is in the units time-1. For further information about first-order reactions, refer to First-Order Reactions.
Ways to Characterize Decay Constant
There are two ways to characterize the decay constant: mean-life and half-life. In both cases the unit of measurement is seconds. As indicated by the name, mean-life is the average of an element's lifetime and can be shown in terms of following expression
\[ N_t=N_o e^{-\lambda t} \label{5} \]
\[1 = \int^{\infty}_ 0 c \cdot N_0 e^{-\lambda t} dt = c \cdot \dfrac{N_0}{\lambda} \label{6}\]
Rearranging the equation:
\[ c= \dfrac{\lambda}{N_o}\]
Decay Rate Half-Life
Half-life is the time period that is characterized by the time it takes for half of the substance to decay (both radioactive and non-radioactive elements).The rate of decay remains constant throughout the decay process. There are three ways to show the exponential nature of half-life.
\[ N_t=N_o\left( \dfrac{1}{2} \right)^{t/t_{1/2}} \label{7} \]
\[ N_t=N_o e^{-t/\tau} \label{8} \]
By comparing Equations 1, 3 and 4, one will get following expressions
\[ \ln {\left( \dfrac{1}{2} \right)^{t/t_{1/2}}}= \ln(e^{-t/\tau}) = \ln (e^{-\lambda t} ) \label{9}\]
or with \(\ln(e) = 1\), then
\[ \dfrac{t}{t_{1/2}} \ln \left( \frac{1}{2} \right) = \dfrac{-t}{\tau} = -\lambda t \label{10}\]
By canceling \(t\) on both sides, one will get following equation (for half-life)
\[t_{1/2}= \dfrac{\ln(2)}{\lambda} \approx \dfrac{0.693}{\lambda} \label{11} \]
or combining equations 1B and 11
\[ A = \dfrac{0.693}{t_{1/2}}N \label{12}\]
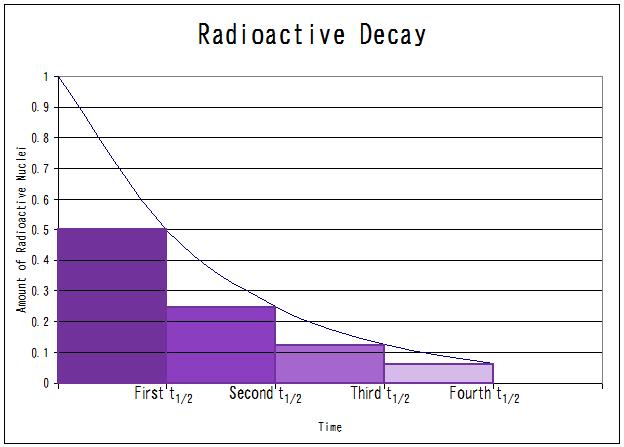
Equation 11 is a constant, meaning the half-life of radioactive decay is constant. Half-life and the radioactive decay rate constant λ are inversely proportional which means the shorter the half-life, the larger \(\lambda\) and the faster the decay. This is a hypothetical radioactive decay graph. If the half-life were shorter, then the exponential decay graph would be steeper and the line would be decreasing at a faster rate; therefore, the amount of the radioactive nuclei would decrease as well.
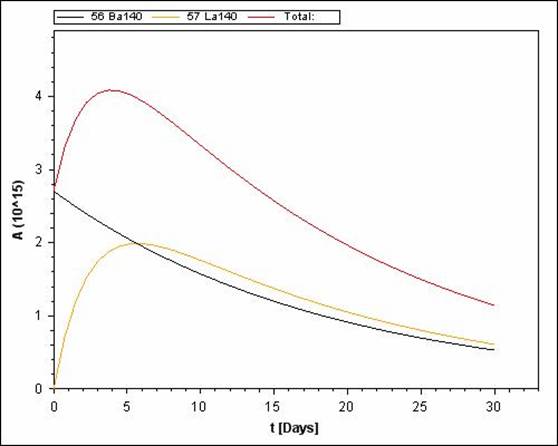
Radioactive decay is not always a one step phenomenon. Often times the parent nuclei changes into a radioactive daughter nuclei which also decays. In such cases, it is possible that the half-life of the parent nuclei is longer or shorter than the half-life of the daughter nuclei. Depending upon the substance, it is possible that both parent and daughter nuclei have similar half lives.
Ba-140 Parent has a longer half-life than the daughter nuclei (La and Ce)
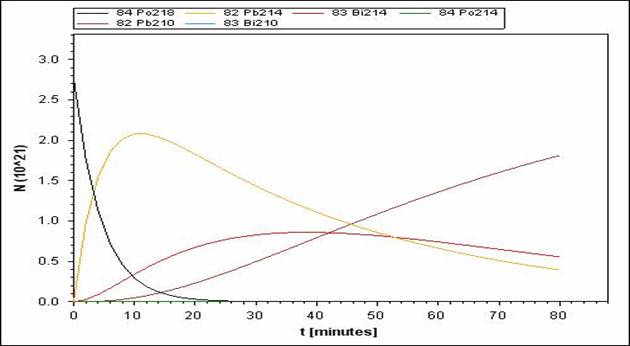
Po-218 has a smaller half-life than its daughter nuclei (different species of Pb and Bi).
Almost equal half-life for both parents (\(^{135}I\)) and daughter nuclei (\(^{135}Xe\) and \(^{135}Cs\))
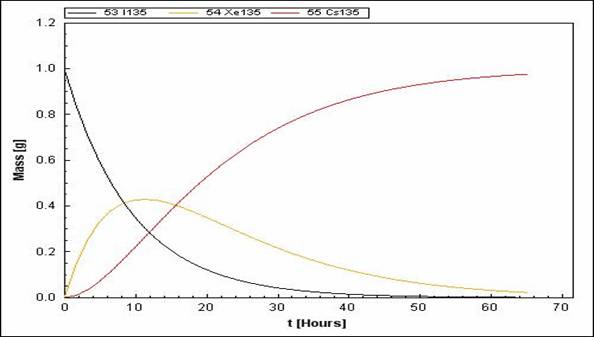
Constant Decay Rate
Since the decay rate is constant, one can use the radioactive decay law and the half-life formula to find the age of organic material, which is known as radioactive dating. One of the forms of radioactive dating is radiocarbon dating. Carbon 14 (C-14) is produced in the upper atmosphere through the collision of cosmic rays with atmospheric 14N. This radioactive carbon is incorporated in plants and respiration and eventually with animals that feed upon plants. The ratio of C-14 to C-12 is 1:10^12 within plants as well as in the atmosphere. This ratio, however, increases upon the death of an animal or when a plant decays because there is no new income of carbon 14. By knowing the half-life of carbon-14 (which is 5730 years) one can calculate the rate of disintegration of the nuclei within the organism or substance and thereby determine its age. It is possible to use other radioactive elements in order to determine the age of nonliving substances as well.
Problems
- Determine the decay constant for Carbon-14, if it has a half-life of 5730 years?
- If Radium-223 has a half life of 10.33 days, what time duration would it require for the activity associated with this sample to decrease 1.5% of its present value?
- Determine the number of atoms in a 1.00 mg sample of Carbon-14?
- What mass of Carbon-14 must be in a sample to have an activity of 2.00 mCi?
- The disintegration rate for a sample Co-60 is 6800 dis/h. If the half-life is 5.3 years, determine the quantity of atoms in this sample?
- Isotope A requires 6.0 days for its decay rate to fall to 1/20 its initial value. Isotope B has a half-life that is 1.5 times that of A. How long will it take for isotope B to decrease to 1/16 of its initial value?
- A sample disintegrates at the following rate of counts per minute (cpm): t=0, 2000 cpm; t=5 hr, 1984 cpm; t=50 hr, 1848 cpm; t=500 hr, 904 cpm; t=1250, 276 cpm. What is the half-life of this nuclide?
Solutions
Odd Problem Solutions:
1. Using Equation 11, we can set \(t_{1/2} = 573\, yrs\) and solve for \(\lambda\).
\[\lambda=1.209 \times 10^{-4}\; yr^{-1}\]
3. To find the number of atoms in a Carbon-14 sample, we will use dimensional analysis. First we convert 1.00mg to 0.001 grams. From the name, we know the atomic mass of Carbon-14 to be 14 g/mol. We know Avogadro's number expresses \(6.022 \times 10^{23}\) atoms. Now we have the equation:
\[ N= \dfrac{0.001\; g}{(1\; mol/14\;g)(6.022 \times 10^{23})} \;atoms/ 1\;mol\]
\(N=4.301 \times 10^{19} \, \text{atoms}\)
5. Using Equation 1B and Equation 12, we can combine them and solve for \(N\). By rearranging Equation 11, \(\lambda=\ln\; 2/t_{1/2}\) we can insert that into Equation 1B. Now we have the formula \(A=\ln 2/t_{1/2} N\). Now we have to convert 5.3 years to hours because the activity is measured in disintegration (atoms) per hour.
\[t_{1/2}=5.3\; \cancel{years} \times \left(\dfrac{365\; \cancel{days}}{1\; \cancel{year}}\right) \times \left(\dfrac{24\;hr}{1\;\cancel{day}} \right)=46,428\; hours\]
From equation 12, \(N\) can be calculated
\[N = A\; \dfrac{t_{1/2}}{\ln 2}\]
or
\[N = (6,800\; dis/hr)\; \dfrac{46,428\; hr}{\ln 2} \approx 4.56 \times 10^8\; \text{atoms}\]
The Cobalt-60 sample has 456,000,000 atoms.
7. We want to determine the decay constant. By looking at the first and last given values, we can use Equation 2 to solve for λ.
\[\ln(276\;cpm / 2000\;cpm)=-\lambda \times 1250\;hr\]
\[\lambda = 0.00158 \;hr^{-1}\]
Then using Equation 11, we can solve for half-life.
\[t_{1/2}=\dfrac{\ln 2}{0.00158}\]
The half-life of the sample is 438 hours.
References
- Chunn-Mei Zhou and Zhen Dong Wu. Calculations of Se79 Decay. Nuclear Science and Techniques. Volume 17(1), 21-23 (2006)
- Dorin N. Poenaru. Nuclear Decay Modes. First edition. Taylor & Francis, 1996.
- Brett Parker. AP Chemistry. First edition. Thomson & Peterson, 2006.
- Petrucci, Harwood, Herring, Madura. General Chemistry: Principles & Modern Applications. Ninth Edition. <state w:st="on"><place w:st="on">New Jersey</place></state>: Pearson Education, 2007.
- Eric G. Hendee, William R Hendee, Geoffrey S. Ibbott. Radiation Therapy Physics. Third Edition. <state w:st="on"><place w:st="on">New Jersey</place></state>: John Wiley & Sons, Inc, 2005.
- Roger. "Nuclear Transformation Equations." Online Video Clip. A and AS Physics Tuition. Accessed on 01 December 2009. <fizzics.co.uk/default.aspx>

