Atomic Radii
- Page ID
- 610
Atomic radii is useful for determining many aspects of chemistry such as various physical and chemical properties. The periodic table greatly assists in determining atomic radius and presents a number of trends.
Definition
Atomic radius is generally stated as being the total distance from an atom’s nucleus to the outermost orbital of electron. In simpler terms, it can be defined as something similar to the radius of a circle, where the center of the circle is the nucleus and the outer edge of the circle is the outermost orbital of electron. As you begin to move across or down the periodic table, trends emerge that help explain how atomic radii change.
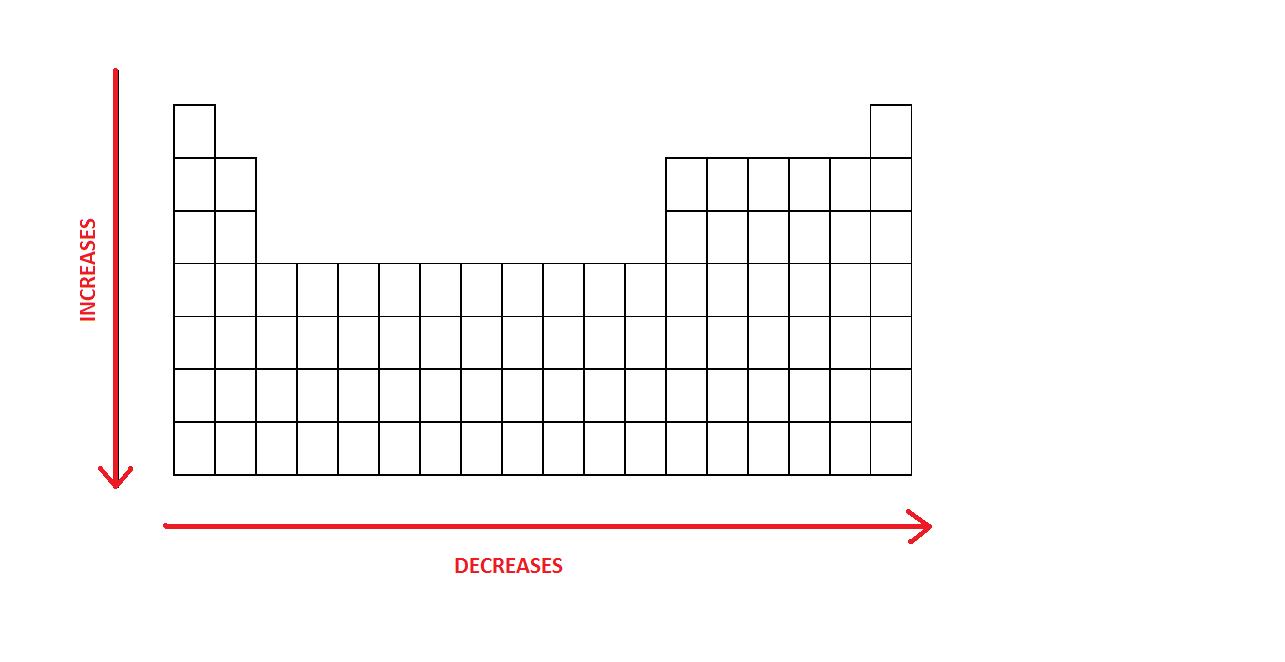
The effective nuclear charge (\(Z_{eff}\)) of an atom is the net positive charge felt by the valence electron. Some positive charge is shielded by the core electrons therefore the total positive charge is not felt by the valence electron. A detailed description of shielding and effective nuclear charge can be found here. \(Z_{eff}\) greatly affects the atomic size of an atom. So as the \(Z_{eff}\) decreases, the atomic radius will grow as a result because there is more screening of the electrons from the nucleus, which decreases the attraction between the nucleus and the electron. Since \(Z_{eff}\)decreases going down a group and right to left across the periodic table, the atomic radius will increase going down a group and right to left across the periodic table.
Types of Radius with Respect to Types of Bonds
Determining the atomic radii is rather difficult because there is an uncertainty in the position of the outermost electron – we do not know exactly where the electron is. This phenomenon can be explained by the Heisenberg Uncertainty Principle. To get a precise measurement of the radius, but still not an entirely correct measurement, we determine the radius based on the distance between the nuclei of two bonded atoms. The radii of atoms are therefore determined by the bonds they form. An atom will have different radii depending on the bond it forms; so there is no fixed radius of an atom.
Covalent Radius
When a covalent bond is present between two atoms, the covalent radius can be determined. When two atoms of the same element are covalently bonded, the radius of each atom will be half the distance between the two nuclei because they equally attract the electrons. The distance between two nuclei will give the diameter of an atom, but you want the radius which is half the diameter.
Covalent radii will increase in the same pattern as atomic radii. The reason for this trend is that the bigger the radii, the further the distance between the two nuclei. See explanation for \(Z_{eff}\) for more details.
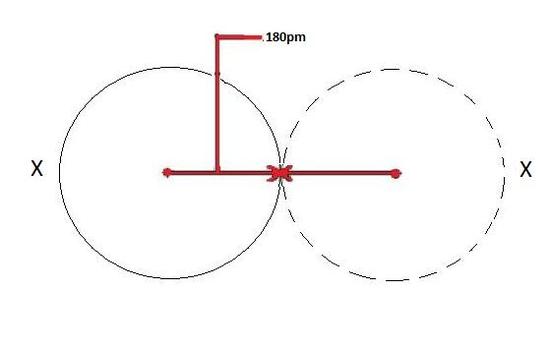
The covalent radius depicted below in Figure 1 will be the same for both atoms because they are of the same element as shown by X.
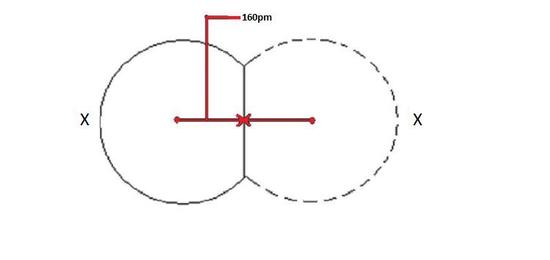
Ionic Radius
The ionic radius is the radius of an atom forming ionic bond or an ion. The radius of each atom in an ionic bond will be different than that in a covalent bond. This is an important concept. The reason for the variability in radius is due to the fact that the atoms in an ionic bond are of greatly different size. One of the atoms is a cation, which is smaller in size, and the other atom is an anion which is a lot larger in size. So in order to account for this difference, one most get the total distance between the two nuclei and divide the distance according to atomic size. The bigger the atomic size, the larger radius it will have. This is depicted in Figure 2 as shown below where the cation is displayed on the left as X+, and clearly has a smaller radius than the anion, which is depicted as Y- on the right.
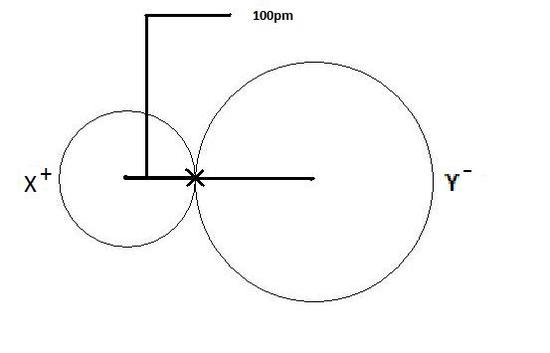
If we were able to determine the atomic radius of an atom from experimentation, say Se, which had an atomic radius of 178 pm, then we could determine the atomic radius of any other atom bonded to Se by subtracting the size of the atomic radius of Se from the total distance between the two nuclei. So, if we had the compound CaSe, which had a total distance of 278 pm between the nucleus of the Ca atom and Se atom, then the atomic radius of the Ca atom will be 278 pm (total distance) - 178 pm (distance of Se), or 100 pm. This process can be applied to other examples of ionic radius.
Cations have smaller ionic radii than their neutral atoms. In contrast, anions have bigger ionic radii than their corresponding neutral atoms.
A detailed explanation is given below:
- The cation, which is an ion with a positive charge, by definition has fewer electrons than protons. The loss in an electron will consequently result in a change in atomic radii in comparison to the neutral atom of interest (no charge).
- The loss of an electron means that there are now more protons than electrons in the atom, which is stated above. This will cause a decrease in atomic size because there are now fewer electrons for the protons to pull towards the nucleus and will result in a stronger pull of the electrons towards the nucleus. It will also decrease because there are now less electrons in the outer shell, which will decrease the radius size.
- An analogy to this can be of a magnet and a metallic object. If ten magnets and ten metallic objects represent a neutral atom where the magnets are protons and the metallic objects are electrons, then removing one metallic object, which is like removing an electron, will cause the magnet to pull the metallic objects closer because of a decrease in number of the metallic objects. This can similarly be said about the protons pulling the electrons closer to the nucleus, which as a result decreases atomic size.
Figure 3 below depicts this process. A neutral atom X is shown here to have a bond length of 180 pm and then the cation X+ is smaller with a bond length of 100 pm.
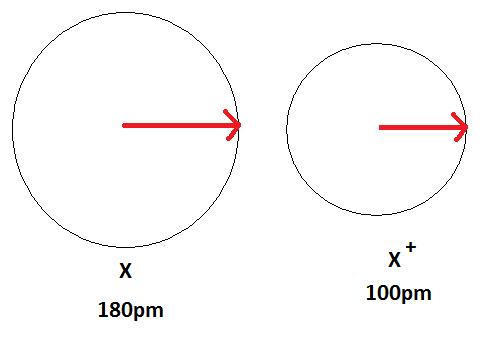
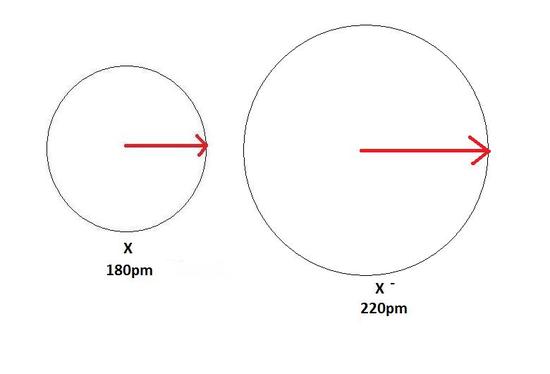
An anion, on the other hand, will be bigger in size than that of the atom it was made from because of a gain of an electron. This can be seen in the Figure 4 below. The gain of an electron adds more electrons to the outermost shell which increases the radius because there are now more electrons further away from the nucleus and there are more electrons to pull towards the nucleus so the pull becomes slightly weaker than of the neutral atom and causes an increase in atomic radius.
Metallic Radius
The metallic radius is the radius of an atom joined by metallic bond. The metallic radius is half of the total distance between the nuclei of two adjacent atoms in a metallic cluster. Since a metal will be a group of atoms of the same element, the distance of each atom will be the same (Figure 5).
Periodic Trends of Atomic Radius
- An atom gets larger as the number of electronic shells increase; therefore the radius of atoms increases as you go down a certain group in the periodic table of elements.
- In general, the size of an atom will decrease as you move from left to the right of a certain period.
The radius of atoms increases as you go down a certain group.
The size of an atom will decrease as you move from left to the right of a period.
EXCEPTIONS: Because the electrons added in the transition elements are added in the inner electron shell and at the same time, the outer shell remains constant, the nucleus attracts the electrons inward. The electron configuration of the transition metals explains this phenomenon. This is why Ga is the same size as its preceding atom and why Sb is slightly bigger than Sn.
References
- Pauling, Linus. Atomic Radii and Interatomic Distances in Metal, Journal of the American Chemical Society 194769 (3), 542-553
- Petrucci, Ralph H., William S. Harwood, Geoffery F. Herring, and Jeffry D. Madura. General Chemistry. 9th ed. New Jersey: Pearsin Prentice Hall, 2007.
Problems
- Which atom is larger: K or Br?
- Which atom is larger: Na or Cl?
- Which atom is smaller: Be or Ba?
- Which atom is larger: K+ or K?
- Put in order of largest to smallest: F, Ar, Sr, Cs.
- Which has a bigger atomic radius: Sr2+ or Se2-?
- If Br has an ionic radius of 100 pm and the total distance between K and Br in KBr is 150 pm, then what is the ionic radius of K?
- Which has a smaller atomic radius: Cs+ or Xe?
- If the distance between the nuclei of two atoms in a metallic bond is 180 pm, what is the atomic radius of one atom?
- If Z effective is increasing, is the atomic radius also increasing?
*Hint* When solving a radius-bond problem, identify the bond first and then use the standard method of finding the radius for that particular bond. Also remember the trend for the atomic radii.
Answers
- K
- Na
- Be
- K
- Cs, Sr, Ar, F
- Se2-
- 50 pm
- Cs+
- 90 pm
- No

