Vapor Pressure
- Page ID
- 22958
Pressure is the average force that material (gas, liquid or solid) exert upon the surface, e.g. walls of a container or other confining boundary. Vapor pressure or equilibrium vapor pressure is the pressure of a vapor in thermodynamic equilibrium with its condensed phases in a closed container. All liquids and solids have a tendency to evaporate or sublime into a gaseous form and all gases have a tendency to condense back to their liquid or solid form.
Introduction
When a liquid is in a confined, closed, container, an equilibrium exists between the liquid and its gaseous phase. This equilibrium exists regardless of the temperature inside the container and the temperature of the liquid. The equilibrium exists due to the fact that some of the particles in the liquid, essentially at any temperature, will always have enough energy to escape the intrinsic cohesive forces and enter the gaseous phase (Figure \(\PageIndex{1}\)).
The vapor pressure of a substance is the pressure that the gaseous part of the substance exerts on the container of said substance.
The fact that the vapor pressure is equal to the external pressure can become important when talking about boiling temperatures at various altitudes. At higher altitudes the pressure is lower than at sea level and therefore liquids such as water boil at lower temperatures. This would translate it into a longer time to cook something in the water as compared to cooking the same object at sea level. The opposite is also true if one boils water at an altitude lower than sea level.
Characteristics of Vapor Pressure
Vapor pressures are dependent only on temperature and nothing else. The vapor pressure of a liquid does not depend on the amount on the liquid in the container, be it one liter or thirty liters; at the same temperature, both samples will have the same vapor pressure. Vapor pressures have an exponential relationship with temperature and always increase as temperature increases (Figure 2: Vapor Pressure Curves). It is important to note that when a liquid is boiling, its vapor pressure is equal to the external pressure. For example, as water boils at sea level, its vapor pressure is 1 atmosphere because the external pressure is also 1 atmosphere.
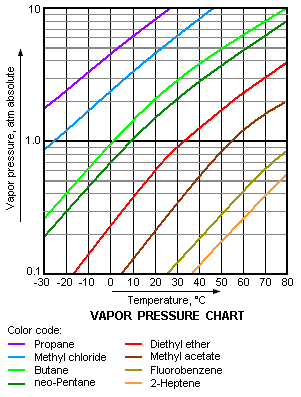
Figure \(\PageIndex{2}\): This chart shows the general relationship between a substance's vapor pressure and temperature change. Generally a substance's vapor pressure increases as temperature increases and decreases as temperature decreases (i.e. vapor pressure is directly proportional to temperature). This chart shows that this trend is true for various substances with differing chemical properties.
The change in vapor pressure of a pure substance as temperature changes can be described using the equation known as the Clausius-Clapeyron Equation:
\[ ln \dfrac{P_2}{P_1} = \dfrac{\Delta H_{vap}}{R} \left ( \dfrac{1}{T_1}-\dfrac{1}{T_2} \right) \label{CC}\]
Where:
- P1 is the partial pressure of the liquid at T1
- P2 is the partial pressure of the liquid at T2
If the vapor pressure of water at 293 K is 17.5 mmHg, what is the vapor pressure of water at 300 K?
Solution
Step 1: Use the Clausius Clapeyron equation (Equation \ref{CC}). Assume 293 K to be T1 and 17.5 mmHg to be P1 and 300 K to be T2. We know the enthalpy of vaporization of water is 44000 J mol-1. Therefore we plug in everything we are given into the equation.
\[ ln\dfrac{P_2}{17.5mmHg} = \dfrac{44000 J mol^{-1}}{8.3145 Jmol^{-1}K^{-1}}\ \left(\dfrac{1}{293K}-\dfrac{1}{300K} \right) \]
Step 2: Calculate everything possible, which is everything on the right side of the equation.
\[ ln \dfrac{P_2}{17.5 mmHg} = (5291.96 K)(0.0000796 K^{-1}) \]
Step 3: To isolate the variable, we need to get rid of the natural log function on the left side. To do so, we must exponentiate both sides of the equation after calculating the numerical value of the right side of the equation:
\[ \dfrac{P_2}{17.5 mmHg} = e^{0.421} \]
Step 4: To solve for P2, we multiply both sides of the equation by 17.5mmHg.
\[ P_2 = 26.7 mmHg \]
The vapor pressure of water at 298K is 23.8 mmHg. At what temperature is the vapor pressure of water 1075 mmHg?
Solution
Step 1: Once again this can be solved using the Clausius-Clapeyron equation. If we set P1 = 23.8 mmHg, T1 = 298K, and P2 = 1075 mmHg, all we need to do is to solve for T2. So plug everything we know into the Clausius-Clapeyron Equation and we get:
\[ \ln\dfrac{1075 mmHg}{23.8 mmHg} = \dfrac{44000 Jmol^{-1}}{8.3145 Jmol^{-1}K^{-1}}\ \left (\dfrac{1}{298 K}-\dfrac{1}{T_2} \right) \]
Step 2: We can solve the right side of the equation for a numerical answer and we can simplify the right side of the equation to:
\[ 3.81 = (5291.96 K)(\dfrac{1}{298K}-\dfrac{1}{T_2}) \]
Step 3: Further simplifying the equation by distributing the 5291.96 K, we get:
\[ 3.81 = (17.76) - \dfrac{5291.96K}{T_{2}} \]
Step 4: After subtracting 17.76 from both sides and multiplying both sides by T2 to isolate the T2 term, we get:
\[ -13.95T_2 = -5291.96K \]
Step 5: Solving for T2 we get:
\[ T_2 = 383K \]
*Note: There may be some slight variations in this answer if you try working this problem out. The rounding in this problem will make a relatively large difference in mmHg (10-20 mmHg).
Vapor Pressure of Solutions: Raoult's Law
While the Clausius-Clapeyron equation is useful for describing the vapor pressure behavior of a pure substance, it does not quite help us when we need to describe the vapor pressure of a solution comprised of two ore more different liquids with different vapor pressures, that is where Raoult's Law comes in. Raoult's Law is:
\[ \displaystyle P_{total} = \sum_{i} P_{i}X_{i} \label{Rlaw} \]
Where Pi is the vapor pressure of that particular substance and Xi is the corresponding mole fraction of that substance. "i" is an indexing component that keeps track of each substance in the solution.

Figure \(\PageIndex{3}\): Raoult's Law is used for calculating the vapor pressure of solutions with two or more substances in it. The total vapor pressure is a function of the vapor pressure of the individual vapor pressures of the components and their respective mole fractions.
Essentially what Raoult's Law states is that the vapor pressure of a solution with two or more components is directly proportional to the vapor pressures of each component and their respective amounts in the solution (Figure 3). However, Raoult's Law is used to describe solutions that are essentially ideal solutions, meaning it is assumed that there are no interactions between the components of the solution. If the solution is non-ideal, it will deviate from the relationship described by Raoult's Law.
A solution is comprised of 0.5000 mole H2O, 1.000 mole ethanol, and 2.000 moles acetaldehyde at 293 K. What is the total vapor pressure of this solution? The partial pressures of these substances at 293 K are, respectively, 18 mmHg, 67.5 mmHg, and 740 mmHg (assume the liquids mix homogeneously).
Solution
Step 1: Calculate the mole fractions (moles of each substance divided by total moles) of each substance in the solution.
\[ X_{water} = 0.5000/3.500 = 0.143 \]
\[ X_{ethanol} = 1.000/3.500 = 0.286 \]
\[ X_{acetaldehyde} = 2.000/3.500 = 0.571 \]
Step 2: Plug in all the values and solve for Ptotal
\[ P_{total} = (18mmHg)(0.143) + (67.5 mmHg)(0.286) + (740mmHg)(0.571mmHg) \]
\[ P_{total} = 444.4 mmHg \]
A solution is comprised of only water and ethylene glycol and is at 293 K. Water's mole fraction in this solution is 0.379 and water's vapor pressure at this temperature is 18 mmHg (assume the water and ethylene glycol mix homogeneously). The total vapor pressure of this solution is 9.15 mmHg. Calculate the vapor pressure of pure ethylene glycol at this temperature.
Solution
Step 1: Since this solution is only comprised of water and ethylene glycol, we can easily calculate the mole fraction of ethylene glycol in this solution by subtracting water's mole fraction from 1.
\[ X_{ethylene glycol} = 1 - 0.379 = 0.621 \]
Step 2: Once we have the mole fraction of ethylene glycol, we have everything we need to solve for the partial pressure of pure ethylene glycol at 293 K using Raoult's Law:
\[ 9.15 = (18mmHg)(0.379) + (P_{ethylene glycol})(0.621) \]
Solving for \(P_{ethylene glycol}\) we get:
\[ P_{ethylene glycol} = 3.75mmHg \]
Henry's Law
Both the Clausius-Clapeyron Equation (Equation \ref{CC}) and Raoult's Law (Equation \ref{Rlaw}) describe liquids without any significant solutes in them. So what happens if the liquid contains a nonvolatile solute, in other words, a solute that does not evaporate and merely stays in the solution? Will the vapor pressure of the liquid increase or decrease? It turns out that having a nonvolatile solute in the liquid will decrease the vapor pressure of the liquid because the solutes will interfere with the high-energy liquid molecules' path to the surface to break free into the gaseous phase. An example of a nonvolatile solute in a liquid would be glucose in water (Figure \(\PageIndex{4}\): Henry's Law).
Henry's Law can also be used the describe the partial pressure of a volatile solute in a liquid as a function of its concentration in the liquid. An example of this would be oxygen or carbon dioxide in a soda. Henry's Law is as follows:
\[ C = (K_{H})P_{gas} \]
Where P is the partial pressure of either the volatile solute or of the solvent with a nonvolatile solute in it and C is the solubility of the volatile solute or the concentration of the solvent with a nonvolatile solute in it. KH is Henry's Constant and is different for various substances and differs with temperature and comes in many different units.
Assume at 273 K and a CO2 pressure of 3.6 atm, the aqueous solubility of CO2 is 24.8 ml CO2 per liter. What is the molarity of a saturated water solution when the CO2 is under its normal partial pressure in air of 0.000395 atm.
Step 1: We need to calculate Henry's Constant for CO2 when the partial pressure of CO2 is 3.6 atm. To do this, we must first calculate the molarity of CO2 under these conditions:
\[ Molarity = \dfrac{0.0248L CO_{2} * \dfrac{1 mol CO_{2}}{22.4L CO_{2}}}{1 L solution} = 0.00111 M CO_{2} \]
Step 2: Next we must solve for Henry's Constant under these conditions:
\[ K_H = \dfrac{C}{P_{CO_2}} = 0.000308 \dfrac{M CO_2}{atm} \]
Step 3: Solve for the concentration (molarity) using Henry's Law:
\[ C = K_H * P_{CO_2} = 0.000308M CO_{2}atm^{-1} * 0.000395atm = 1.22 M CO_2 \]
One great use of Henry's Law is to calculate the various solubilities of gases in solutions under different pressures. One example of this is what is colloquially referred to as "the bends" (scientifically called decompression sickness). When divers go underwater, they are subjected to much higher pressures than they would be at sea level therefore their blood is much more soluble to gases and as such much larger quantities of gases such as nitrogen dissolve in the blood. If the divers then rise up back to the surface too quickly, these gases will be forced out of their dissolved form and form bubbles in the blood vessels. These gas bubbles can then cause the blood vessels to pop, causing much physical pain and serious medical issues. To avoid this, divers rise from deep depths slowly so their bodies can expel the extraneous gas through the lungs and allow the amounts of gas in the blood to equilibrate with the external pressure. This way the divers can avoid gas bubbles forming in blood vessels and therefore any personal injury.

Problems
The vapor pressure of water at 283 K is 9.2 mmHg, at what temperature is the vapor pressure of water 546 mmHg?
- At 393 K the vapor pressure of water is 1489 mmHg; what is the vapor pressure of water at 343 K?
- A solution's partial pressure is 34.93 mmHg. This solution is comprised of Chemical A and Chemical B. The partial pressure of Chemical A is 24.5 mmHg and its mole fraction is .145. What is the partial pressure of Chemical B?
- Chemical A's partial pressure is 35.5 mmHg and Chemical B's partial pressure is 895.5 mmHg. Their respective mole fractions are 0.79 and 0.21. What is the the partial pressure of a homogenous solution of Chemical A and Chemical B?
- Assume at 273 K and an O2 pressure of 4.7 atm, the aqueous solubility of CO2 is 79.6 ml CO2 per liter. What is the molarity of a saturated water solution when the CO2 is under its normal partial pressure in air of 0.21 atm.
Answers
- 364K
- 233.7mmHg
- 36.7mmHg
- 216.1mmHg
- 0.000159 M O2
References
- Petrucci, et al. General Chemistry: Principles & Modern Applications; Ninth Edition. Pearson/Prentice Hall; Upper Saddle River, New Jersey 07.
- Brown, et al. Chemistry: The Central Science; Tenth Edition. Pearson/Prentice Hall; New Jersey 2005.
- Wilmhurst PT, Byrne JC, and MM Webb-Peploe. "Relation between interartrial shunts and decompression sickness in divers." The Lancet (1989). Web. 27 February 2010
Contributors and Attributions
- Shuyang (Scott), Liu (UCD), Caroline Tran

