Bohr's Hydrogen Atom
- Page ID
- 1687
Niels Bohr introduced the atomic Hydrogen model in 1913. He described it as a positively charged nucleus, comprised of protons and neutrons, surrounded by a negatively charged electron cloud. In the model, electrons orbit the nucleus in atomic shells. The atom is held together by electrostatic forces between the positive nucleus and negative surroundings.
Hydrogen Energy Levels
The Bohr model is used to describe the structure of hydrogen energy levels. The image below represents shell structure, where each shell is associated with principal quantum number n. The energy levels presented correspond with each shell. The amount of energy in each level is reported in eV, and the maxiumum energy is the ionization energy of 13.598eV.
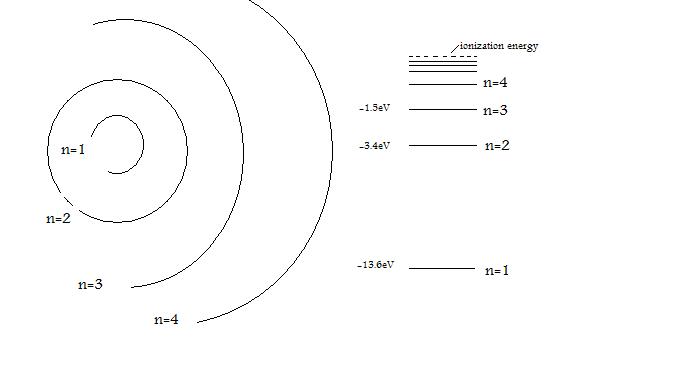
Figure 1: Some of the orbital shells of a Hydrogen atom. The energy levels of the orbitals are shown to the right.
Hydrogen Spectrum
The movement of electrons between these energy levels produces a spectrum. The Balmer equation is used to describe the four different wavelengths of Hydrogen which are present in the visible light spectrum. These wavelengths are at 656, 486, 434, and 410nm. These correspond to the emission of photons as an electron in an excited state transitions down to energy level n=2. The Rydberg formula, below, generalizes the Balmer series for all energy level transitions. To get the Balmer lines, the Rydberg formula is used with an nf of 2.
Rydberg Formula
The Rydberg formula explains the different energies of transition that occur between energy levels. When an electron moves from a higher energy level to a lower one, a photon is emitted. The Hydrogen atom can emit different wavelengths of light depending on the initial and final energy levels of the transition. It emits a photon with energy equal to the difference of square of the final (\(n_f\)) and initial (\(n_i\)) energy levels.
\[\text{Energy}=R\left(\dfrac{1}{n^2_f}-\dfrac{1}{n^2_i}\right) \label{1}\]
The energy of a photon is equal to Planck’s constant, h=6.626*10-34m2kg/s, times the speed of light in a vacuum, divided by the wavelength of emission.
\[E=\dfrac{hc}{\lambda} \label{2}\]
Combining these two equations produces the Rydberg Formula.
\[\dfrac{1}{\lambda}=R\left(\dfrac{1}{n^2_f}-\dfrac{1}{n^2_i}\right) \label{3}\]
The Rydberg Constant (R) = \(10,973,731.6\; m^{-1}\) or \(1.097 \times 10^7\; m^{-1}\).
Limitations of the Bohr Model
The Bohr Model was an important step in the development of atomic theory. However, it has several limitations.
- It is in violation of the Heisenberg Uncertainty Principle. The Bohr Model considers electrons to have both a known radius and orbit, which is impossible according to Heisenberg.
- The Bohr Model is very limited in terms of size. Poor spectral predictions are obtained when larger atoms are in question.
- It cannot predict the relative intensities of spectral lines.
- It does not explain the Zeeman Effect, when the spectral line is split into several components in the presence of a magnetic field.
- The Bohr Model does not account for the fact that accelerating electrons do not emit electromagnetic radiation.
References
- Bohr, Niels. "On the Constitution of Atoms and Molecules, Part I." Philosophical Magazine26 (1913): 1-24. <http://web.ihep.su/dbserv/compas/src/bohr13/eng.pdf>
- Bohr, Niels. "On the Constitution of Atoms and Molecules, Part II." Philosophical Magazine 26 (1913): 476-502. <http://web.ihep.su/dbserv/compas/src/bohr13b/eng.pdf>
- Turner, J. E. Atoms, Radiation, and Radiation Protection. Weinheim: Wiley-VCH, 2007. Print.
Problems
1. An emission spectrum gives one of the lines in the Balmer series of the hydrogen atom at 410 nm. This wavelength results from a transition from an upper energy level to n=2. What is the principal quantum number of the upper level?
2. The Bohr model of the atom was able to explain the Balmer series because:
- larger orbits required electrons to have more negative energy in order to match the angular momentum.
- differences between the energy levels of the orbits matched the difference between energy levels of the line spectra.
- electrons were allowed to exist only in allowed orbits and nowhere else.
- none of the above
3. One reason the Bohr model of the atom failed was because it did not explain why
- accelerating electrons do not emit electromagnetic radiation.
- moving electrons have a greater mass.
- electrons in the orbits of an atom have negative energies.
- electrons in greater orbits of an atom have greater velocities.
Answers
1. (1/λ) = R*[ 1/(22) - 1/(n2) ] , R=1.097x107 m-1 , λ=410nm
(1/410nm) = (1.097x107 m-1) * [ 1/(22) - 1/(n2) ]
[ (1/4.10x10-7m) / (1.097x107 m-1) ] - [ (1/4) ] = [ -1/(n2) ]
-1/-0.02778 = n2
36 = n2 , n=6 --> The emission resulted from a transition from energy level 6 to energy level 2.
2. (B) differences between the energy levels of the orbits matched the difference between energy levels of the line spectra.
3. (A) accelerating electrons do not emit electromagnetic radiation.
Contributors and Attributions
- Michelle Faust

