Dipole-Dipole Interactions
- Page ID
- 1658
Dipole-Dipole interactions result when two dipolar molecules interact with each other through space. When this occurs, the partially negative portion of one of the polar molecules is attracted to the partially positive portion of the second polar molecule. This type of interaction between molecules accounts for many physically and biologically significant phenomena such as the elevated boiling point of water.
Definition of a Dipole
Molecular dipoles occur due to the unequal sharing of electrons between atoms in a molecule. Those atoms that are more electronegative pull the bonded electrons closer to themselves. The buildup of electron density around an atom or discreet region of a molecule can result in a molecular dipole in which one side of the molecule possesses a partially negative charge and the other side a partially positive charge. Molecules with dipoles that are not canceled by their molecular geometry are said to be polar.
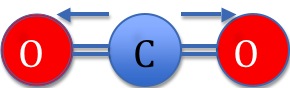
In Figure 1 above, the more electronegative Oxygen atoms pull electron density towards themselves as demonstrated by the arrows. Carbon Dioxide is not polar however because of its linear geometry. A molecule's overall dipole is directional, and is given by the vector sum of the dipoles between the atoms. If we imagined the Carbon Dioxide molecule centered at 0 in the XY coordinate plane, the molecule's overall dipole would be given by the following equation:
\[\mu \cos(0) + -\mu \cos(0) = 0. \]
Where \(μ\) is the dipole moment of the bond (given by μ=Q x r where Q is the charge and r is the distance of separation). Therefore, the two dipoles cancel each other out to yield a molecule with no net dipole.
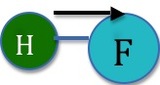
In contrast, figure 2 demonstrates a situation where a molecular dipole does result. There is no opposing dipole moment to cancel out the one that is shown above. If we were to imagine the hydrogen flouride molecule placed so that the Hydrogen sat at the origin in the XY coordinate plane, the dipole would be given by \(\mu \cos(0)=\mu\).
Potential Energy of Dipole Interaction
Potential energy is the maximum energy that is available for an object to do work. In physics, work is a quantity that describes the energy expended as a force operates over a distance. Potential energy is positional because it depends on the forces acting on an object at its position in space. For instance, we could say that an object held above the ground has a potential energy equal to its mass x acceleration due to gravity x its height above the ground (i.e., \(mgh\)). This potential energy that an object has as a result of its position can be used to do work. For instance we could use a pulley system with a large weight held above the ground to hoist a smaller weight into the air. As we drop the large weight it converts its potential energy to kinetic energy and does work on the rope which lifts the smaller weight into the air. It is important to remember that due to the second law of thermodynamics, the amount of work done by an object can never exceed (and is often considerably less) than the objects potential energy.
On a subatomic level, charged atoms have an electric potential which allows them to interact with each other. Electric potential refers to the energy held by a charged particle as a result of it's position relative to a second charged particle. Electric potential depends on charge polarity, charge strength and distance. Molecules with the same charge will repel each other as they come closer together while molecules with opposite charges will attract.
For two positively charged particles interacting at a distance r, the potential energy possessed by the system can be defined using Coulomb's Law:
\[V = \dfrac{kQq}{r} \label{1}\]
where
- \(k\) is the Coulomb constant and
- \(Q\) and \(q\) refer to the magnitude of the charge for each particle in Coulombs.
The above equation can also be used to calculate the distance between two charged particles (\(r\)) if we know the potential energy of the system. While Coulomb's law is important, it only gives the potential energy between two point particles. Since molecules are much larger than point particles and have charge concentrated over a larger area, we have to come up with a new equation.
The potential energy possessed by two polar atoms interacting with each other depends on the dipole moment, μ, of each molecule, the distance apart, r, and the orientation in which the two molecules interact. For the case in which the partially positive area of one molecule interacts only with the partially negative area of the other molecule, the potential energy is given by:
\[V(r) = -\dfrac{2\mu_{1}\mu_{2}}{4\pi\epsilon_{o}r^{3}} \label{2}\]
where \(\epsilon_o\) is the permeability of space. If it is not the case that the molecular dipoles interact in this straight end to end manor, we have to account mathematically for the change in potential energy due to the angle between the dipoles. We can add an angular term to the above equation to account for this new parameter of the system:
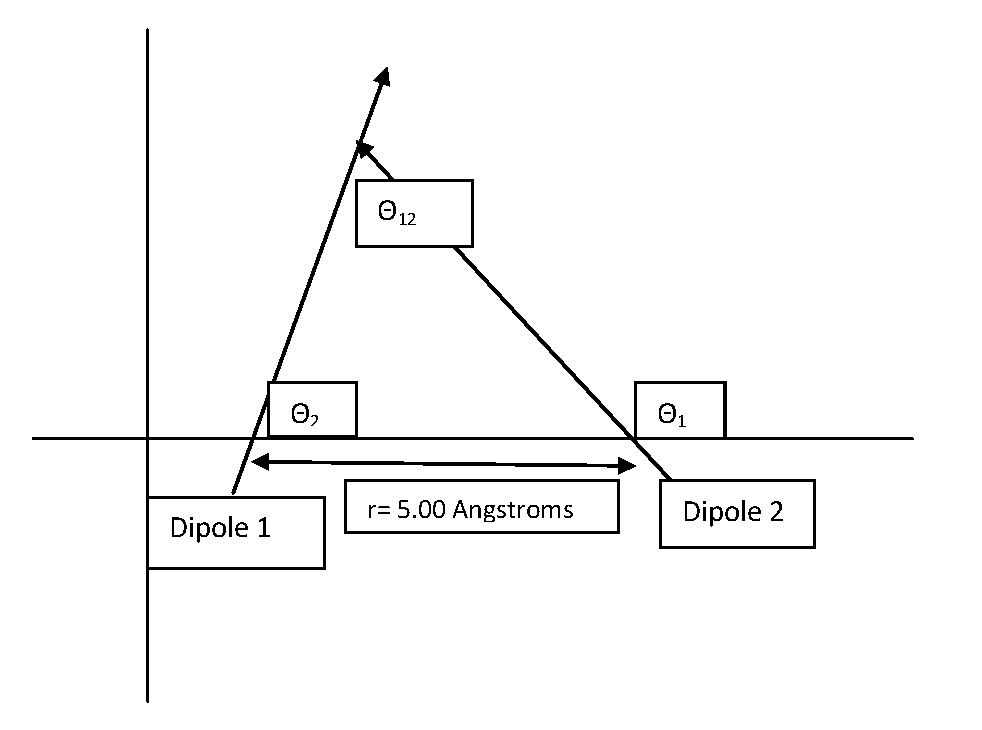
\[V (r) =-\dfrac{\mu_{1}\mu_{2}}{4\pi\epsilon_{0}r_{12}^{3}}{(\cos\theta_{12}- 3\cos\theta_{1}\cos\theta_{2})} \label{3}\]
In this formula \(\theta_{12}\) is the angle made by the two oppositely charged dipoles, and \(r_{12}\) is the distance between the two molecules. Also, \(\theta_{1}\) and \(\theta_{2}\) are the angles formed by the two dipoles with respect to the line connecting their centers.
It is also important to find the potential energy of the dipole moment for more than two interacting molecules. An important concept to keep in mind when dealing with multiple charged molecules interacting is that like charges repel and opposite charges attract. So for a system in which three charged molecules (2 positively charged molecules and 1 negatively charged molecule) are interacting, we need to consider the angle between the attractive and repellant forces.
The potential energy for the dipole interaction between multiple charged molecules is:
\[V = \dfrac{kp \cos\theta}{r^{2}} \label{4}\]
where
- \(k\) is the Coulomb constant, and
- \(r\) is the distance between the molecules.

Calculate the potential energy of the dipole-dipole interaction between 2 \(\ce{HF}\) molecules oriented along the x axis in an XY coordinate plane whose area of positive charge is separated by 5.00 Angstroms from the area of negative charge of the adjacent molecule:
Solution
The Dipole moment of the HF molecules can be found in many tables, μ=1.92 D. Assume the molecules exist in a vacuum such that \(\epsilon_{0}=8.8541878\times10^{-12}C^2N^{-1}m^{-2}\)
\[\mu=1.92D\times3.3356\times10^{-30}\dfrac{Cm}{D}=6.4044\times10^{-30}Cm\]
Now use Equation \ref{2} to calculate the interaction energy
\[\begin{align*}V&=-\dfrac{2(6.4044\times10^{-30}Cm)^2}{4(8.8541878\times10^{-12}C^2N^{-1}m^{-2})(5.0\times10^{-10})^3} \\[4pt] &=1.4745\times10^{-19}Nm \end{align*}\]
Now imagine the same two HF molecules in the following orientation:
Given: \(\theta_{1}=\dfrac{3\pi}{4}\), \(\theta_{2}=\dfrac{\pi}{3}\) and \(\theta_{12}=\dfrac{5\pi}{12}\)
Solution
\[\begin{align*} V&=-\dfrac{(6.4044\times10^{-30}Cm)^2}{4\pi(8.8541878\times10^{-12}C^2N^{-1}m^{-2}(5.00\times10^{-10}m)^3}(\cos\dfrac{5\pi}{12}-3\cos\dfrac{3\pi}{4}\cos\dfrac{\pi}{3}) \\[4pt] &=-9.73\times10^{-20}Nm=9.73\times10^{-20}J\end{align*}\]
Dipole-Dipole Interactions in Macroscopic Systems
It would seem, based on the above discussion, that in a system composed of a large number of dipolar molecules randomly interacting with one another, V should go to zero because the molecules adopt all possible orientations. Thus the negative potential energy of two molecular dipoles participating in a favorable interaction would be cancelled out by the positive energy of two molecular dipoles participating in a high potential energy interaction. Contrary to our assumption, in bulk systems, it is more probable for dipolar molecules to interact in such a way as to minimize their potential energy (i.e., dipoles form less energetic, more probable configurations in accordance with the Boltzmann's Distribution). For instance, the partially positive area of a molecular dipole being held next to the partially positive area of a second molecular dipole is a high potential energy configuration and few molecules in the system will have sufficient energy to adopt it at room temperature. Generally, the higher potential energy configurations are only able to be populated at elevated temperatures. Therefore, the interactions of dipoles in a bulk Solution are not random, and instead adopt more probable, lower energy configurations. The following equation takes this into account:
\[V=-\dfrac{2\mu_{A}^2\mu_{B}^2}{3(4\pi\epsilon_{0})^2r^6}\dfrac{1}{k_{B}T} \label{5}\]
Looking at Equation \ref{5}, what happens to the potential energy of the interaction as temperature increases.
Solution
The potential energy of the dipole-dipole interaction decreases as T increases. This can be seen from the form of the above equation, but an explanation for this observation is relatively simple to come by. As the temperature of the system increases, more molecules have sufficient energy to occupy the less favorable configurations. The higher, less favorable, configurations are those that give less favorable interactions between the dipoles (i.e., higher potential energy configurations).
Calculate the average energy of HF molecules interacting with one another in a bulk Solution assuming that the molecules are 4.00 Angstroms apart in room temperature Solution.
Solution
Using Equation \ref{5} to calculate the bulk potential energy:
\[\begin{align*} V&=-\dfrac{2}{3}\dfrac{(6.4044\times10^{-30}Cm)^4}{(4\pi(8.8541878\times10^{-12}C^2N^{-1}m^{-2})^2(4.00\times10^{-10}m)^6}\dfrac{1}{(1.381\times10^{-23}Jk^{-1})(298k)} \\[4pt] &=-5.46\times10^{-21}J\end{align*}\]
What is the amount of energy stabilization that is provided to the system when 1 mole of HF atoms interact through dipole-dipole interactions.
Solution
Since we have already calculated above the average potential energy of the HF dipole-dipole interaction this problem can be easily solved.
\[\begin{align*} V &=-5.46\times10^{-21}J\times(6.022\times10^{23}mol^{-1}) \\[4pt] &=-3288\dfrac{J}{mol}=3.29\dfrac{kJ}{mol} \end{align*}\]
The potential energy from dipole interactions is important for living organisms. The biggest impact dipole interactions have on living organisms is seen with protein folding. Every process of protein formation, from the binding of individual amino acids to secondary structures to tertiary structures and even the formation of quaternary structures is dependent on dipole-dipole interactions.
A prime example of quaternary dipole interaction that is vital to human health is the formation of erythrocytes. Erythrocytes, commonly known as red blood cells are the cell type responsible for the gas exchange (i.e. respiration). Inside the erythrocytes, the molecule involved in this crucial process, is 'hemoglobin', formed by four protein subunits and a heme group'. For an heme to form properly, multiple steps must occur, all of which involve dipole interactions. The four protein subunits—two alpha chains, two beta chains—and the heme group, interact with each other through a series of dipole-dipole interactions which allow the erythrocyte to take its final shape. Any mutation that destroys these dipole-dipole interactions prevents the erythrocyte from forming properly, and impairs their ability to carry oxygen to the tissues of the body. So we can see that without the dipole-dipole interactions, proteins would not be able to fold properly and all life as we know it would cease to exist.
References
- Le Fèvre, R. J. W. (1953). Dipole moments; their measurement and application in chemistry. London, Methuen.
- Atkins, P. W. and J. De Paula (2006). Physical chemistry for the life sciences. New York, Oxford University Press ; Freeman.
- Petrucci, R. H., W. S. Harwood, et al. (2002). General chemistry : principles and modern applications. Upper Saddle River, N.J., Prentice Hall.
- Bloomfield, M. M. (1992). Chemistry and the living organism. New York, Wiley.
- Silbey, R. J., R. A. Alberty, et al. (2005). Physical chemistry. Hoboken, NJ, Wiley.
- HyperPhysics. http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html Georgia State University, Department of Physics and Astronomy. 2008.
- Campbell, N. A. and J. B. Reece (2005). Biology. San Francisco, Pearson Benjamin Cummings.
- Chang, Raymond. (2005). Physical Chemistry for the Biosciences. Sausalito, California, University Science Books.