9.1: The Schrödinger Equation For Multi-Electron Atoms
- Page ID
- 4536
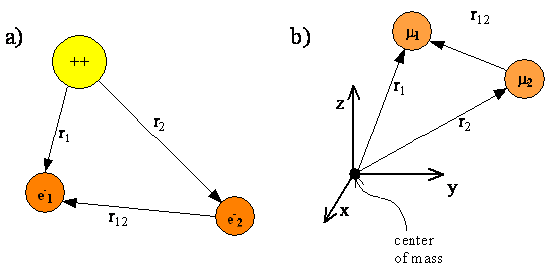
In this chapter, we will use the helium atom as a specific example of a multi-electron atom. Figure \(\PageIndex{1}\) shows a schematic representation of a helium atom with two electrons whose coordinates are given by the vectors \(r_1\) and \(r_2\). The electrons are separated by a distance \(r_{12} = |r_1-r_2|\). The origin of the coordinate system is fixed at the nucleus. As with the hydrogen atom, the nuclei for multi-electron atoms are so much heavier than an electron that the nucleus is assumed to be the center of mass. Fixing the origin of the coordinate system at the nucleus allows us to exclude translational motion of the center of mass from our quantum mechanical treatment.
The Hamiltonian operator for the hydrogen atom serves as a reference point for writing the Hamiltonian operator for atoms with more than one electron. Start with the same general form we used for the hydrogen atom Hamiltonian
\[\hat {H} = \hat {T} + \hat {V} \label {9-1}\]
Include a kinetic energy term for each electron and a potential energy term for the attraction of each negatively charged electron for the positively charged nucleus and a potential energy term for the mutual repulsion of each pair of negatively charged electrons. The He atom Hamiltonian is
\[ \hat {H} = -\dfrac {\hbar ^2}{2m_e} (\nabla ^2_1 + \nabla ^2_2) + V (r_1) + V (r_2) + V (r_{12}) \label {9-2}\]
where
\[ V(r_1) = -\dfrac {2e^2}{4 \pi \epsilon _0 r_1} \label {9-3}\]
\[ V(r_2) = -\dfrac {2e^2}{4 \pi \epsilon _0 r_2} \label {9-4}\]
\[ V(r_{12}) = +\dfrac {e^2}{4 \pi \epsilon _0 r_{12}} \label {9-5}\]
Equation \(\ref{9-2}\) can be extended to any atom or ion by including terms for the additional electrons and replacing the He nuclear charge +2 with a general charge \(Z\); e.g.
\[V(r_1) = -\dfrac {Ze^2}{4 \pi \epsilon _0 r_1} \label {9-6}\]
Equation \(\ref{9-2}\) then becomes
\[\hat {H} = -\dfrac {\hbar ^2}{2m_e} \sum _i \nabla ^2_i + \sum _i V (r_i) + \sum _{i \ne j} V (r_{ij}) \label {9-7}\]
Exercise \(\PageIndex{1}\)
Referring to Equation \(\ref{9-7}\), explain the meaning of the three summations and write expressions for the \(V(r_i)\) and \(V(r_{ij})\) terms.
Exercise \(\PageIndex{2}\)
Write the multi-electron Hamiltonian (e.g. Equation \(\ref{9-2}\)) for a boron atom.
Each electron has its own kinetic energy term in Equations \(\ref{9-2}\) and \(\ref{9-7}\). For an atom like sodium there would be \(\nabla ^2_1 , \nabla ^2_2 , \cdot , \nabla ^2_{11}\). The other big difference between single electron systems and multi-electron systems is the presence of the \(V(r_{ij})\) terms which contain \(1/r_{ij}\), where \(r_{ij}\) is the distance between electrons \(i\) and \(j\). These terms account for the electron-electron repulsion that we expect between like-charged particles.
Given what we have learned from the previous quantum mechanical systems we’ve studied, we predict that exact solutions to the multi-electron Schrödinger equation in Equation \(\ref{9-7}\) would consist of a family of multi-electron wavefunctions, each with an associated energy eigenvalue. These wavefunctions and energies would describe the ground and excited states of the multi-electron atom, just as the hydrogen wavefunctions and their associated energies describe the ground and excited states of the hydrogen atom. We would predict quantum numbers to be involved, as well.
The fact that electrons interact through their Coulomb repulsion means that an exact wavefunction for a multi-electron system would be a single function that depends simultaneously upon the coordinates of all the electrons; i.e., a multi-electron wavefunction, \(\psi (r_1, r_2, \cdots r_i)\). The modulus squared of such a wavefunction would describe the probability of finding the electrons (though not specific ones) at a designated location in the atom. Alternatively, \(ne |\psi |^2\) would describe the total amount of electron density that would be present at a particular spot in the multi-electron atom. All of the electrons are described simultaneously by a multi-electron wavefunction, so the total amount of electron density represented by the wavefunction equals the number of electrons in the atom.
All of the electrons are described simultaneously by a multi-electron wavefunction, so the total amount of electron density represented by the wavefunction equals the number of electrons in the atom.
Unfortunately, the Coulomb repulsion terms make it impossible to find an exact solution to the Schrödinger equation for many-electron atoms and molecules even if there are only two electrons. The most basic approximations to the exact solutions involve writing a multi-electron wavefunction as a simple product of single-electron wavefunctions, and obtaining the energy of the atom in the state described by that wavefunction as the sum of the energies of the one-electron components.
\[\psi (r_1, r_2, \cdots , r_i) \approx \varphi _1 (r_1) \varphi _2 (r_2) \cdots \varphi _i(r_i) \label {9-8}\]
By writing the multi-electron wavefunction as a product of single-electron functions, we conceptually transform a multi-electron atom into a collection of individual electrons located in individual orbitals whose spatial characteristics and energies can be separately identified. For atoms these single-electron wavefunctions are called atomic orbitals. For molecules, as we will see in the next chapter, they are called molecular orbitals. While a great deal can be learned from such an analysis, it is important to keep in mind that such a discrete, compartmentalized picture of the electrons is an approximation, albeit a powerful one.


