18.11: The Equipartition Principle
- Page ID
- 57608
The equipartition theorem, also known as the law of equipartition, equipartition of energy or simply equipartition, states that every degree of freedom that appears only quadratically in the total energy has an average energy of \(½k_BT\) in thermal equilibrium and contributes \(½k_B\) to the system's heat capacity. Here, \(k_B\) is the Boltzmann constant, and T is the temperature in Kelvin. The law of equipartition of energy states that each quadratic term in the classical expression for the energy contributes ½kBT to the average energy. For instance, the motion of an atom has three degrees of freedom (number of ways of absorbing energy), corresponding to the x, y and z components of its momentum. Since these momenta appear quadratically in the kinetic energy, every atom has an average kinetic energy of \(3/2k_BT\) in thermal equilibrium. The number of degrees of freedom of a polyatomic gas molecule is \(3N\) where \(N\) is the number of atoms in the molecule. This is equal to number of coordinates for the system; e.g. for two atoms you would have x, y, z for each atom.
Translations
The translational contribution to the average energy is derived in terms of the derivative of the translational partition:
\[ \langle E_{trans} \rangle = - \dfrac{1}{q_{trans}} \dfrac{\partial q_{trans}}{\partial \beta} \label{Eq1} \]
Introducing the translational partition function derived earlier, Equation \(\ref{Eq1}\) becomes
\[= - \dfrac{\Lambda^3}{V} \dfrac{\partial }{\partial \beta} \dfrac{V}{\Lambda^3} = - \dfrac{3}{\Lambda} \dfrac{\partial \Lambda}{\partial \beta} = \dfrac{3}{2} k_BT \nonumber \]
Thus, the three translational degrees of freedom in three dimensions satisfy the equipartition theorem with each translational degree providing \( ½ k_BT\) of energy.
Rotations
Consider the molecular partition functions. The average rotational energy to the average energy is derived in terms of the derivative of the translational partition:
\[ \langle E_{rot} \rangle = - \dfrac{1}{q_{rot}} \dfrac{\partial q_{rot}}{\partial \beta} \label{Eq2} \]
which when you introduce the rotational partition function, Equation \(\ref{Eq2}\) becomes
\[ \langle E_{rot} \rangle = -\sigma \beta \tilde{B} \dfrac{1}{\sigma \tilde{B}} \dfrac{\partial}{\partial \beta} \dfrac{1}{\beta} = \dfrac{1}{\beta} = k_BT \nonumber \]
The classical expression for the rotational energy of a diatomic molecule is
\[ E_{rot}^{(classical)}= \dfrac{1}{2} I (\omega_x^2 + \omega_y^2) \nonumber \]
where \(I\) is the moment of inertia and \( \omega _x\) and \( \omega _y\) are the angular velocities in the \(x\) and \(y\) directions. The rotation along the molecular axis (the \(z\) axis here) has no meaning in quantum mechanics because the rotations along the molecular axis lead to configurations which are indistinguishable from the original configuration. The two rotational degrees of freedom have thus given a value of \(kT\) with with each rotational degree providing \( ½ k_BT\) of energy.
Vibrations
Consider vibrational motions. The average vibrational energy to the average energy is derived in terms of the derivative of the translational partition:
\[ \langle E_{vib} \rangle = - \dfrac{1}{q_{vib}} \dfrac{\partial q_{vib}}{\partial \beta} \label{Eq3} \]
which when you introduce the partition function for vibration, Equation \(\ref{Eq3}\) becomes
\[ \langle E_{vib} \rangle = \dfrac{-1}{q_{vib}} \left( -hc\tilde{\nu}\dfrac{ e^{-hc \tilde{\nu}/k_BT}}{(1-e^{-hc \tilde{\nu}/k_BT})^2 } \right) = hc\tilde{\nu} \dfrac{ e^{-hc \tilde{\nu}/k_BT}}{\left(1-e^{-hc \tilde{\nu}/k_BT}\right) } \label{18.1.7} \]
This can be simplified by dividing both numerator and denominator of Equation \(\ref{18.1.7}\) by \(e^{-hc \tilde{\nu}/k_BT}\)
\[\langle E_{vib} \rangle = hc \tilde{\nu} \left( \dfrac{ 1 }{e^{hc \tilde{\nu}/k_BT} -1} \right) \label{18.1.7B} \]
Equation \(\ref{18.1.7B}\) is applicable at all temperatures, but if \( hc \tilde{\nu}/k_BT \ll 1\) (i.e., the high temperature limit), then the exponential in the denominator can be expanded
\[ e^{hc \tilde{\nu}/k_BT} -1 \approx 1 + hc \tilde{\nu}/k_BT -1 = hc \tilde{\nu}/k_BT \label{expansion} \]
and Equation \(\ref{18.1.7B}\) becomes
\[ \langle E_{vib} \rangle \approx \cancel{hc \tilde{\nu}} \left( \dfrac{1}{\cancel{ hc \tilde{\nu}}/k_BT}\right) \nonumber \]
\[ \langle E_{vib} \rangle \approx k_BT \label{18.1.10} \]
with each vibrational degree providing \( k_BT\) of energy (since there ar two quadratic terms in the Hamiltonian for a harmonic oscillator (kinetics energy and potential energy).
Compare Equation \(\ref{18.1.10}\) with the classical expression for the vibrational energy
\[ E_{vib}^{(classical)} = ½ kx^2 + ½ μv_x^2 \nonumber \]
At high temperature the equipartition theorem is valid, but at low temperature, the expansion in Equation \(\ref{expansion}\) fails (or more terms are required). In this case, only a few vibrational states are occupied and the equipartition principle is not typically applicable.
Heat Capacity
Heat capacity at constant volume \(C_v\), is defined as
\[ C_v = \left(\dfrac{\partial U}{\partial T} \right)_v \nonumber \]
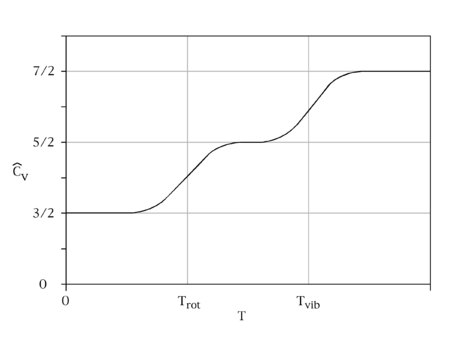
The equipartition theorem requires that each degree of freedom that appears only quadratically in the total energy has an average energy of ½kBT in thermal equilibrium and, thus, contributes ½kB to the system's heat capacity. Thus the three translational degrees of freedom each contribute ½R to (3/2 R). The contribution of rotational kinetic energy will be R for the linear, and 3/2R for the nonlinear molecules. For the vibration, an oscillator has quadratic kinetic and potential terms, making the contribution of each vibrational mode R. However, kBT has to be much greater than the spacing between the quantum energy levels. If this is not satisfied, the heat capacity will be reduced and which drop to zero at low temperatures. The corresponding degree of freedom is said to be frozen out; this is the situation for the vibrational degrees of freedom at room temperature and that is why the usual assumption is that they will not contribute.
For comparing the molar heat capacities of nitrogen dioxide and carbon dioxide at constant volume (at room temperature), let us use the law of equipartition and assume the vibrations to be frozen out at room temperature. The predicted molar for the linear \(CO_2\) (with three translational and two rotational degrees of freedom) is \(5/2R\) \(20.8\, JK^{-1}mo'^{-1})\).
The estimated molar for \(NO_2\) (a bent molecule, with three translational and three rotational degrees of freedom) is \(3R \,(25.0\, JK^{-1}mol^{-1})\). These estimations are close to the experimental values:
- 30.1 JK-1 mol-1 for \(CO_2\)
- 29.5 JK-1 mol-1 for \(NO_2\)
Especially for \(CO_2\), the deviation is significant. This suggests that, although not all vibrational degrees of freedom are available, they cannot be totally ignored. The bigger deviation in the prediction of molar heat capacities is probably due to the existence of the lower frequency-bending vibration in carbon dioxide.
References
- Thermodynamics and Statistical Mechanics, Greiner W., Neise, Stocker, Springer, 2001
- Physical Chemistry, 5th ed., Atkins P., W. H. Freeman and Company, 1994.
Contributors and Attributions
- Zane Sterkewolf (UC Davis)
- www.chem.iitb.ac.in/~bltembe/pdfs/ch_3.pdf
- Sudarson S Sinha (Tel Aviv University)

