Hess's Law
- Page ID
- 1964
Hess's Law of Constant Heat Summation (or just Hess's Law) states that regardless of the multiple stages or steps of a reaction, the total enthalpy change for the reaction is the sum of all changes. This law is a manifestation that enthalpy is a state function.
Introduction
Hess's Law is named after Russian Chemist and Doctor Germain Hess. Hess helped formulate the early principles of thermochemistry. His most famous paper, which was published in 1840, included his law on thermochemistry. Hess's law is due to enthalpy being a state function, which allows us to calculate the overall change in enthalpy by simply summing up the changes for each step of the way, until product is formed. All steps have to proceed at the same temperature and the equations for the individual steps must balance out. The principle underlying Hess's law does not just apply to Enthalpy and can be used to calculate other state functions like changes in Gibbs' Energy and Entropy.
The heat of any reaction \(\Delta{H^°_f}\) for a specific reaction is equal to the sum of the heats of reaction for any set of reactions which in sum are equivalent to the overall reaction:
(Although we have not considered the restriction, applicability of this law requires that all reactions considered proceed under similar conditions: we will consider all reactions to occur at constant pressure.)
Application
Hydrogen gas, which is of potential interest nationally as a clean fuel, can be generated by the reaction of carbon (coal) and water:
\[C_{(s)} + 2 H_2O_{(g)} \rightarrow CO_{2\, (g)} + 2 H_{2\, (g)} \tag{2}\]
Calorimetry reveals that this reaction requires the input of 90.1 kJ of heat for every mole of \(C_{(s)}\) consumed. By convention, when heat is absorbed during a reaction, we consider the quantity of heat to be a positive number: in chemical terms, \(q > 0\) for an endothermic reaction. When heat is evolved, the reaction is exothermic and \(q < 0\) by convention.
It is interesting to ask where this input energy goes when the reaction occurs. One way to answer this question is to consider the fact that the reaction converts one fuel, \(C_{(s)}\), into another, \(H_{2(g)}\). To compare the energy available in each fuel, we can measure the heat evolved in the combustion of each fuel with one mole of oxygen gas. We observe that
\[C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)} \tag{3}\]
produces \(393.5\, kJ\) for one mole of carbon burned; hence \(q=-393.5\, kJ\). The reaction
\[2 H_{2(g)} + O_{2(g)} \rightarrow 2 H_2O_{(g)} \tag{4}\]
produces 483.6 kJ for two moles of hydrogen gas burned, so q=-483.6 kJ. It is evident that more energy is available from combustion of the hydrogen fuel than from combustion of the carbon fuel, so it is not surprising that conversion of the carbon fuel to hydrogen fuel requires the input of energy. Of considerable importance is the observation that the heat input in equation [2], 90.1 kJ, is exactly equal to the difference between the heat evolved, -393.5 kJ, in the combustion of carbon and the heat evolved, -483.6 kJ, in the combustion of hydrogen. This is not a coincidence: if we take the combustion of carbon and add to it the reverse of the combustion of hydrogen, we get
\[C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)}\]
\[2 H_2O_{(g)} \rightarrow 2 H_{2(g)} + O_{2(g)}\]
\[C_{(s)} + O_{2(g)} + 2 H_2O_{(g)} \rightarrow CO_{2(g)} + 2 H_{2(g)} + O_{2(g)} \tag{5}\]
Canceling the \(O_{2(g)}\) from both sides, since it is net neither a reactant nor product, equation [5] is equivalent to equation [2]. Thus, taking the combustion of carbon and "subtracting" the combustion of hydrogen (or more accurately, adding the reverse of the combustion of hydrogen) yields equation [2]. And, the heat of the combustion of carbon minus the heat of the combustion of hydrogen equals the heat of equation [2]. By studying many chemical reactions in this way, we discover that this result, known as Hess's Law, is general.
Why it works
A pictorial view of Hess's Law as applied to the heat of equation [2] is illustrative. In figure 1, the reactants C(s) + 2 H2O(g) are placed together in a box, representing the state of the materials involved in the reaction prior to the reaction. The products CO2(g) + 2 H2(g) are placed together in a second box representing the state of the materials involved after the reaction. The reaction arrow connecting these boxes is labeled with the heat of this reaction. Now we take these same materials and place them in a third box containing C(s), O2(g), and 2 H2(g). This box is connected to the reactant and product boxes with reaction arrows, labeled by the heats of reaction in equation [3] and equation [4].
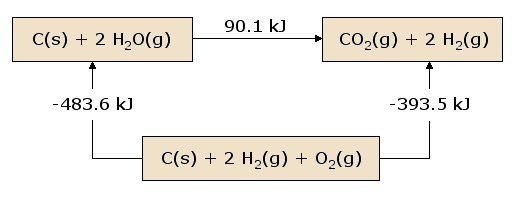
This picture of Hess's Law reveals that the heat of reaction along the "path" directly connecting the reactant state to the product state is exactly equal to the total heat of reaction along the alternative "path" connecting reactants to products via the intermediate state containing \(C_{(s)}\), \(O_{2(g)}\), and 2 \(H_{2(g)}\). A consequence of our observation of Hess's Law is therefore that the net heat evolved or absorbed during a reaction is independent of the path connecting the reactant to product (this statement is again subject to our restriction that all reactions in the alternative path must occur under constant pressure conditions).
A slightly different view of figure 1 results from beginning at the reactant box and following a complete circuit through the other boxes leading back to the reactant box, summing the net heats of reaction as we go. We discover that the net heat transferred (again provided that all reactions occur under constant pressure) is exactly zero. This is a statement of the conservation of energy: the energy in the reactant state does not depend upon the processes which produced that state. Therefore, we cannot extract any energy from the reactants by a process which simply recreates the reactants. Were this not the case, we could endlessly produce unlimited quantities of energy by following the circuitous path which continually reproduces the initial reactants.
By this reasoning, we can define an energy function whose value for the reactants is independent of how the reactant state was prepared. Likewise, the value of this energy function in the product state is independent of how the products are prepared. We choose this function, H, so that the change in the function, ΔH = Hproducts - Hreactants, is equal to the heat of reaction q under constant pressure conditions. H, which we call the enthalpy, is a state function, since its value depends only on the state of the materials under consideration, that is, the temperature, pressure and composition of these materials.
The concept of a state function is somewhat analogous to the idea of elevation. Consider the difference in elevation between the first floor and the third floor of a building. This difference is independent of the path we choose to get from the first floor to the third floor. We can simply climb up two flights of stairs, or we can climb one flight of stairs, walk the length of the building, then walk a second flight of stairs. Or we can ride the elevator. We could even walk outside and have a crane lift us to the roof of the building, from which we climb down to the third floor. Each path produces exactly the same elevation gain, even though the distance traveled is significantly different from one path to the next. This is simply because the elevation is a "state function". Our elevation, standing on the third floor, is independent of how we got to the third floor, and the same is true of the first floor. Since the elevation thus a state function, the elevation gain is independent of the path. Now, the existence of an energy state function H is of considerable importance in calculating heats of reaction. Consider the prototypical reaction in subfigure 2.1, with reactants R being converted to products P. We wish to calculate the heat absorbed or released in this reaction, which is ΔH. Since H is a state function, we can follow any path from R to P and calculate ΔH along that path. In subfigure 2.2, we consider one such possible path, consisting of two reactions passing through an intermediate state containing all the atoms involved in the reaction, each in elemental form. This is a useful intermediate state since it can be used for any possible chemical reaction. For example, in figure 1, the atoms involved in the reaction are C, H, and O, each of which are represented in the intermediate state in elemental form. We can see in subfigure 2.2 that the ΔH for the overall reaction is now the difference between the ΔH in the formation of the products P from the elements and the ΔH in the formation of the reactants R from the elements.

The ΔH values for formation of each material from the elements are thus of general utility in calculating ΔH for any reaction of interest. We therefore define the standard formation reaction for reactant R, as
elements in standard state 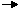 R
R
and the heat involved in this reaction is the standard enthalpy of formation, designated by ΔHf°. The subscript f, standing for "formation," indicates that the ΔH is for the reaction creating the material from the elements in standard state. The superscript ° indicates that the reactions occur under constant standard pressure conditions of 1 atm. From subfigure 2.2, we see that the heat of any reaction can be calculated from
\[\Delta{H^°_f} = \Delta{H^°_{f,products}} -\Delta{H^°_{f,reactants}} \tag{6}\]
Extensive tables of ΔH°f values (Table T1) have been compiled that allows us to calculate with complete confidence the heat of reaction for any reaction of interest, even including hypothetical reactions which may be difficult to perform or impossibly slow to react.
The enthalpy of a reaction does not depend on the elementary steps, but on the final state of the products and initial state of the reactants. Enthalpy is an extensive property and hence changes when the size of the sample changes. This means that the enthalpy of the reaction scales proportionally to the moles used in the reaction. For instance, in the following reaction, one can see that doubling the molar amounts simply doubles the enthalpy of the reaction.
H2 (g) + 1/2O2 (g) → H2O (g) ΔH° = -572 kJ
2H2 (g) + O2 (g) → 2H2O (g) ΔH° = -1144kJ
The sign of the reaction enthalpy changes when a process is reversed.
H2 (g) + 1/2O2 (g) → H2O (g) ΔH° = -572 kJ
When switched:
H2O (g) → H2 (g) + 1/2O2 (g) ΔH° = +572 kJ
Since enthalpy is a state function, it is path independent. Therefore, it does not matter what reactions one uses to obtain the final reaction.
Contributors and Attributions
- Shelly Cohen (UCD)

