5.2: Enthalpy
- Page ID
- 6313
The Learning Objectives of this module is
- To know the key features of a state function.
- To use Hess’s law and thermochemical cycles to calculate enthalpy changes of chemical reactions.
To study the flow of energy during a chemical reaction, we need to distinguish between a system, the small, well-defined part of the universe in which we are interested (such as a chemical reaction), and its surroundings, the rest of the universe, including the container in which the reaction is carried out (Figure 5.5). In the discussion that follows, the mixture of chemical substances that undergoes a reaction is always the system, and the flow of heat can be from the system to the surroundings or vice versa.
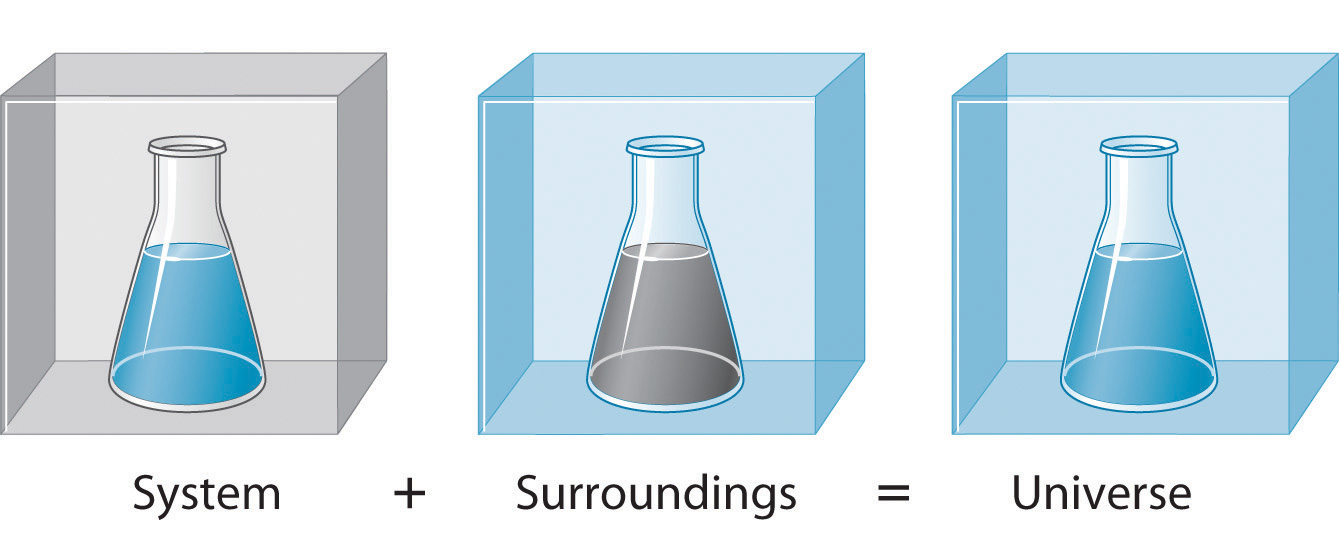
Figure 5.5. A System and Its SurroundingsThe system is that part of the universe we are interested in studying, such as a chemical reaction inside a flask. The surroundings are the rest of the universe, including the container in which the reaction is carried out.
Three kinds of systems are important in chemistry. An open system can exchange both matter and energy with its surroundings. A pot of boiling water is an open system because a burner supplies energy in the form of heat, and matter in the form of water vapor is lost as the water boils. A closed system can exchange energy but not matter with its surroundings. The sealed pouch of a ready-made dinner that is dropped into a pot of boiling water is a closed system because thermal energy is transferred to the system from the boiling water but no matter is exchanged (unless the pouch leaks, in which case it is no longer a closed system). An isolated system exchanges neither energy nor matter with the surroundings. Energy is always exchanged between a system and its surroundings, although this process may take place very slowly. A truly isolated system does not actually exist. An insulated thermos containing hot coffee approximates an isolated system, but eventually the coffee cools as heat is transferred to the surroundings. In all cases, the amount of heat lost by a system is equal to the amount of heat gained by its surroundings and vice versa. That is, the total energy of a system plus its surroundings is constant, which must be true if energy is conserved.
The state of a system is a complete description of a system at a given time, including its temperature and pressure, the amount of matter it contains, its chemical composition, and the physical state of the matter. A state function is a property of a system whose magnitude depends on only the present state of the system, not its previous history. Temperature, pressure, volume, and potential energy are all state functions. The temperature of an oven, for example, is independent of however many steps it may have taken for it to reach that temperature. Similarly, the pressure in a tire is independent of how often air is pumped into the tire for it to reach that pressure, as is the final volume of air in the tire. Heat and work, on the other hand, are not state functions because they are path dependent. For example, a car sitting on the top level of a parking garage has the same potential energy whether it was lifted by a crane, set there by a helicopter, driven up, or pushed up by a group of students (Figure 5.6). The amount of work expended to get it there, however, can differ greatly depending on the path chosen. If the students decided to carry the car to the top of the ramp, they would perform a great deal more work than if they simply pushed the car up the ramp (unless, of course, they neglected to release the parking brake, in which case the work expended would increase substantially!). The potential energy of the car is the same, however, no matter which path they choose.
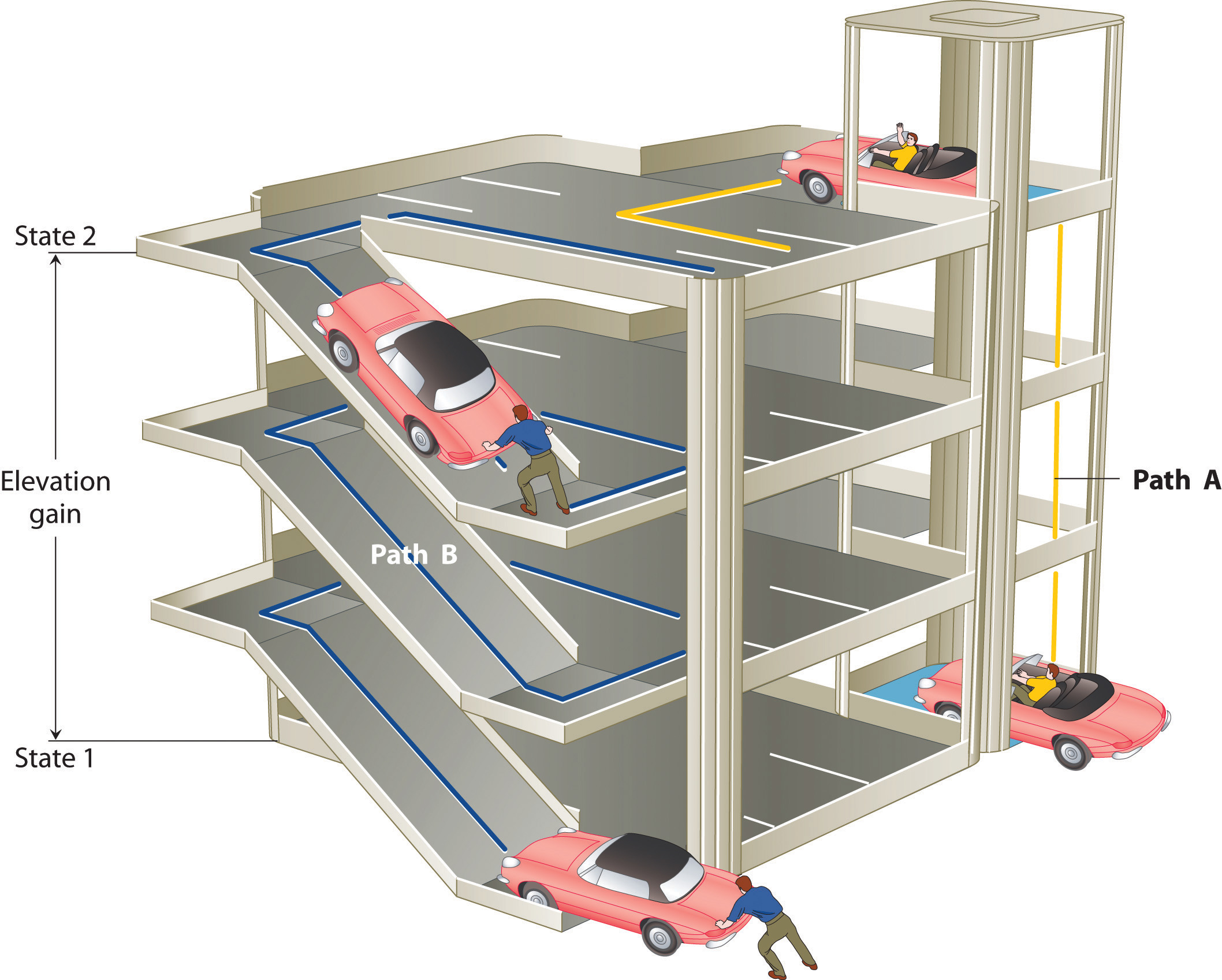
Figure 5.6 Elevation as an Example of a State Function. The change in elevation between state 1 (at the bottom of the parking garage) and state 2 (at the top level of the parking garage) is the same for both paths A and B; it does not depend on which path is taken from the bottom to the top. In contrast, the distance traveled and the work needed to reach the top do depend on which path is taken. Elevation is a state function, but distance and work are not state functions.
Direction of Heat Flow
The reaction of powdered aluminum with iron(III) oxide, known as the thermite reaction, generates an enormous amount of heat—enough, in fact, to melt steel (see chapter opening image). The balanced chemical equation for the reaction is as follows:
\[ 2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s) \tag{5.8}\]
We can also write this chemical equation as
\[2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s) + \text{heat} \tag{5.9}\]
to indicate that heat is one of the products. Chemical equations in which heat is shown as either a reactant or a product are called thermochemical equations. In this reaction, the system consists of aluminum, iron, and oxygen atoms; everything else, including the container, makes up the surroundings. During the reaction, so much heat is produced that the iron liquefies. Eventually, the system cools; the iron solidifies as heat is transferred to the surroundings. A process in which heat (q) is transferred from a system to its surroundings is described as exothermic. By convention, q < 0 for an exothermic reaction.
When you hold an ice cube in your hand, heat from the surroundings (including your hand) is transferred to the system (the ice), causing the ice to melt and your hand to become cold. We can describe this process by the following thermochemical equation:
\[ heat + H_2O(s) \rightarrow H2O(l) \tag{5.10}\]
When heat is transferred to a system from its surroundings, the process is endothermic. By convention, q > 0 for an endothermic reaction.
Enthalpy of Reaction
We have stated that the change in energy (ΔE) is equal to the sum of the heat produced and the work performed (Equation 5.3). Work done by an expanding gas is called pressure-volume work, also called PV work. Consider, for example, a reaction that produces a gas, such as dissolving a piece of copper in concentrated nitric acid. The chemical equation for this reaction is as follows:
\[Cu_{(s)} + 4HNO_{3(aq)} \rightarrow Cu(NO_3)_{2(aq)} + 2H_2O_{(l)} + 2NO_{2(g)} \tag{5.11}\]
If the reaction is carried out in a closed system that is maintained at constant pressure by a movable piston, the piston will rise as nitrogen dioxide gas is formed (Figure 5.7). The system is performing work by lifting the piston against the downward force exerted by the atmosphere (i.e., atmospheric pressure). We find the amount of PV work done by multiplying the external pressure P by the change in volume caused by movement of the piston (ΔV). At a constant external pressure (here, atmospheric pressure)
\[w = −PΔV \tag{5.12}\]
The negative sign associated with PV work done indicates that the system loses energy. If the volume increases at constant pressure (ΔV > 0), the work done by the system is negative, indicating that a system has lost energy by performing work on its surroundings. Conversely, if the volume decreases (ΔV < 0), the work done by the system is positive, which means that the surroundings have performed work on the system, thereby increasing its energy.
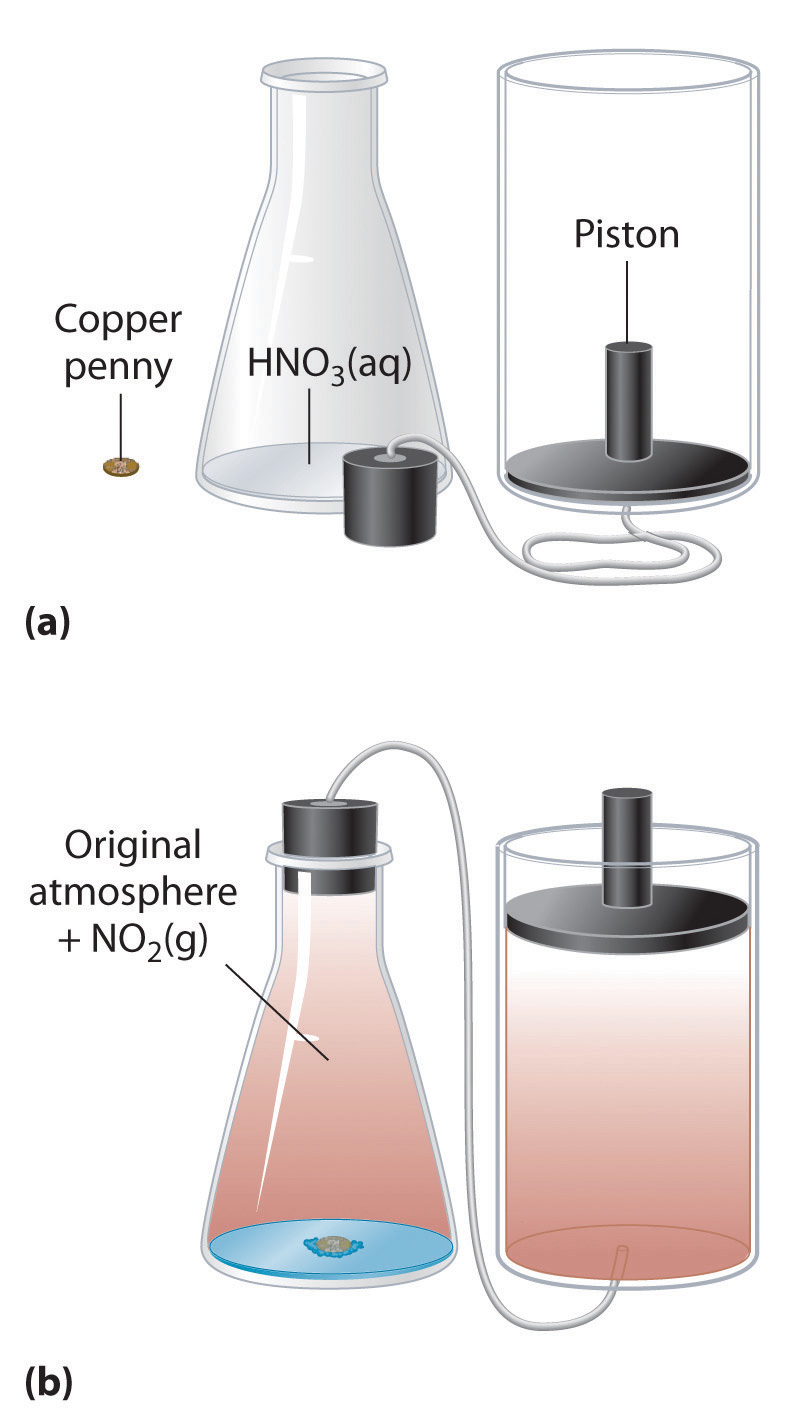
Figure 5.7 An Example of Work Performed by a Reaction Carried Out at Constant Pressure. (a) Initially, the system (a copper penny and concentrated nitric acid) is at atmospheric pressure. (b) When the penny is added to the nitric acid, the volume of NO2 gas that is formed causes the piston to move upward to maintain the system at atmospheric pressure. In doing so, the system is performing work on its surroundings.
The symbol E in Equation 5.3 represents the internal energy of a system, which is the sum of the kinetic energy and potential energy of all its components. It is the change in internal energy that produces heat plus work. To measure the energy changes that occur in chemical reactions, chemists usually use a related thermodynamic quantity called enthalpy (H) (from the Greek enthalpein, meaning “to warm”). The enthalpy of a system is defined as the sum of its internal energy E plus the product of its pressure P and volume V:
\[H = E + PV \tag{5.13}\]
Because internal energy, pressure, and volume are all state functions, enthalpy is also a state function.
If a chemical change occurs at constant pressure (for a given P, ΔP = 0), the change in enthalpy (ΔH) is
\[ ΔH = Δ(E + PV) = ΔE + ΔPV = ΔE + PΔV\tag{5.14}\]
Substituting q + w for ΔE (Equation 5.3) and −w for PΔV (Equation 5.12), we obtain
\[ΔH = ΔE + PΔV = q_p + w − w = q_p \tag{5.15}\]
The subscript p is used here to emphasize that this equation is true only for a process that occurs at constant pressure. From Equation 5.15 we see that at constant pressure the change in enthalpy, ΔH of the system, defined as Hfinal − Hinitial, is equal to the heat gained or lost.
\[ΔH = H_{final} − H_{initial} = q_p \tag{5.16}\]
Just as with ΔE, because enthalpy is a state function, the magnitude of ΔH depends on only the initial and final states of the system, not on the path taken. Most important, the enthalpy change is the same even if the process does not occur at constant pressure.
| Note |
|---|
| To find \(ΔH\)for a reaction, measure \(q_p\). |
When we study energy changes in chemical reactions, the most important quantity is usually the enthalpy of reaction (ΔHrxn), the change in enthalpy that occurs during a reaction (such as the dissolution of a piece of copper in nitric acid). If heat flows from a system to its surroundings, the enthalpy of the system decreases, so ΔHrxn is negative. Conversely, if heat flows from the surroundings to a system, the enthalpy of the system increases, so ΔHrxn is positive. Thus ΔHrxn < 0 for an exothermic reaction, and ΔHrxn > 0 for an endothermic reaction. In chemical reactions, bond breaking requires an input of energy and is therefore an endothermic process, whereas bond making releases energy, which is an exothermic process. The sign conventions for heat flow and enthalpy changes are summarized in the following table:
| Reaction Type | q | ΔHrxn |
|---|---|---|
| exothermic | < 0 | < 0 (heat flows from a system to its surroundings) |
| endothermic | > 0 | > 0 (heat flows from the surroundings to a system) |
If ΔHrxn is negative, then the enthalpy of the products is less than the enthalpy of the reactants; that is, an exothermic reaction is energetically downhill (part (a) in Figure 5.8). Conversely, if ΔHrxn is positive, then the enthalpy of the products is greater than the enthalpy of the reactants; thus, an endothermic reaction is energetically uphill (part (b) in Figure 5.8). Two important characteristics of enthalpy and changes in enthalpy are summarized in the following discussion.
| Note |
|---|
| Bond breaking ALWAYS requires an input of energy; bond making ALWAYS releases energy. |
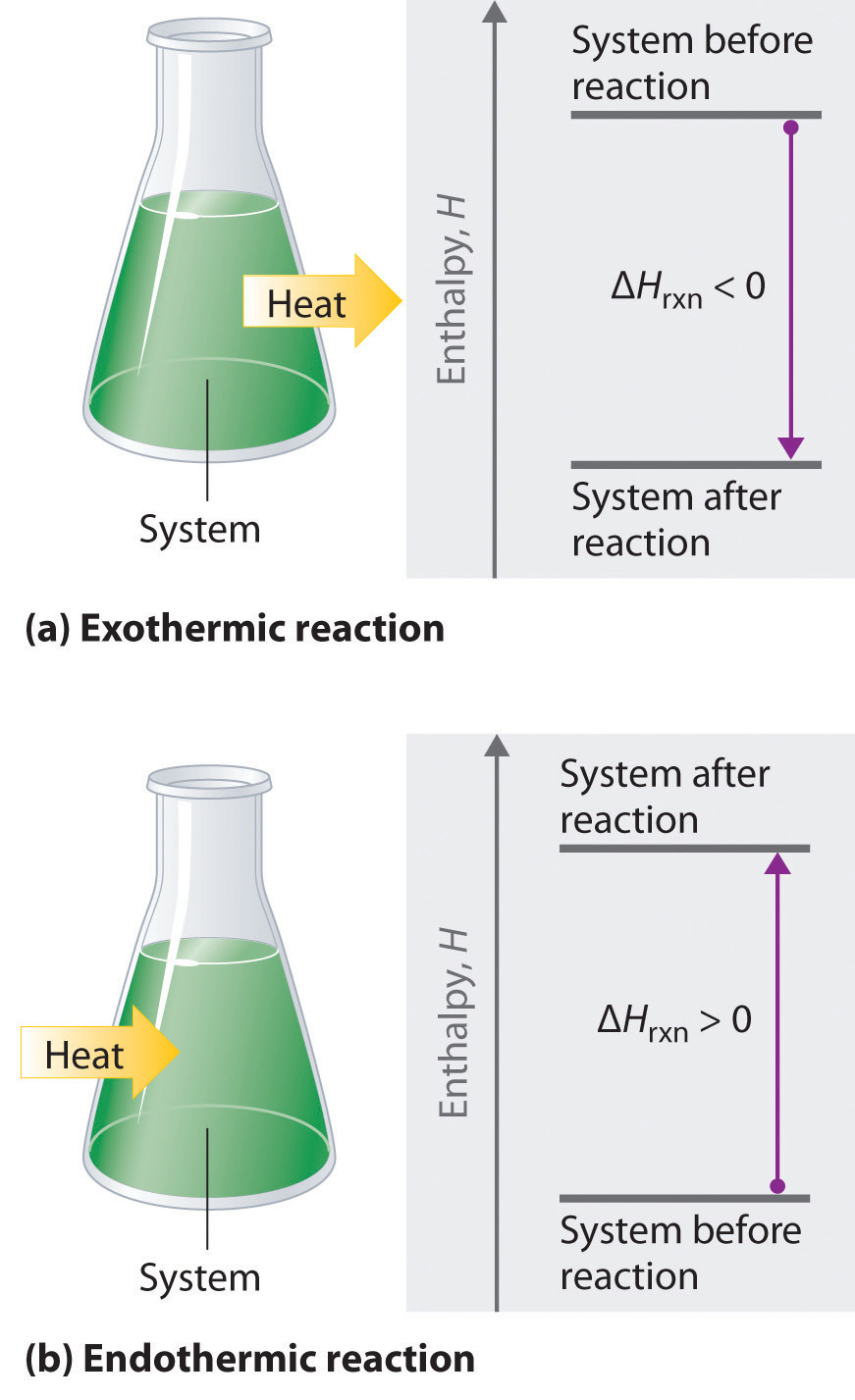
Figure 5.8 The Enthalpy of Reaction. Energy changes in chemical reactions are usually measured as changes in enthalpy. (a) If heat flows from a system to its surroundings, the enthalpy of the system decreases, ΔHrxn is negative, and the reaction is exothermic; it is energetically downhill. (b) Conversely, if heat flows from the surroundings to a system, the enthalpy of the system increases, ΔHrxn is positive, and the reaction is endothermic; it is energetically uphill.
-
Reversing a reaction or a process changes the sign of ΔH. Ice absorbs heat when it melts (electrostatic interactions are broken), so liquid water must release heat when it freezes (electrostatic interactions are formed):
Equation 5.17
Equation 5.18
In both cases, the magnitude of the enthalpy change is the same; only the sign is different.
-
Enthalpy is an extensive property (like mass). The magnitude of ΔH for a reaction is proportional to the amounts of the substances that react. For example, a large fire produces more heat than a single match, even though the chemical reaction—the combustion of wood—is the same in both cases. For this reason, the enthalpy change for a reaction is usually given in kilojoules per mole of a particular reactant or product. Consider Equation 5.19, which describes the reaction of aluminum with iron(III) oxide (Fe2O3) at constant pressure. According to the reaction stoichiometry, 2 mol of Fe, 1 mol of Al2O3, and 851.5 kJ of heat are produced for every 2 mol of Al and 1 mol of Fe2O3 consumed:
\[2Al(s) + Fe_2O_{3(s)} \rightarrow 2Fe(s) + Al_2O_{3(s)} + 851.5 kJ \tag{5.19}\]Thus ΔH = −851.5 kJ/mol of Fe2O3. We can also describe ΔH for the reaction as −425.8 kJ/mol of Al: because 2 mol of Al are consumed in the balanced chemical equation, we divide −851.5 kJ by 2. When a value for ΔH, in kilojoules rather than kilojoules per mole, is written after the reaction, as in Equation 5.20, it is the value of ΔH corresponding to the reaction of the molar quantities of reactants as given in the balanced chemical equation:
Equation 5.20
If 4 mol of Al and 2 mol of Fe2O3 react, the change in enthalpy is 2 × (−851.5 kJ) = −1703 kJ. We can summarize the relationship between the amount of each substance and the enthalpy change for this reaction as follows:
Equation 5.21
The relationship between the magnitude of the enthalpy change and the mass of reactants is illustrated in Example 2.
| Example 1 |
|---|
| Certain parts of the world, such as southern California and Saudi Arabia, are short of freshwater for drinking. One possible solution to the problem is to tow icebergs from Antarctica and then melt them as needed. If ΔH is 6.01 kJ/mol for the reaction H2O(s) → H2O(l) at 0°C and constant pressure, how much energy would be required to melt a moderately large iceberg with a mass of 1.00 million metric tons (1.00 × 106 metric tons)? (A metric ton is 1000 kg.) Given: energy per mole of ice and mass of iceberg Asked for: energy required to melt iceberg Strategy: A Calculate the number of moles of ice contained in 1 million metric tons (1.00 × 106 metric tons) of ice. B Calculate the energy needed to melt the ice by multiplying the number of moles of ice in the iceberg by the amount of energy required to melt 1 mol of ice. Solution: A Because enthalpy is an extensive property, the amount of energy required to melt ice depends on the amount of ice present. We are given ΔH for the process—that is, the amount of energy needed to melt 1 mol (or 18.015 g) of ice—so we need to calculate the number of moles of ice in the iceberg and multiply that number by ΔH (+6.01 kJ/mol): B The energy needed to melt the iceberg is thus Because so much energy is needed to melt the iceberg, this plan would require a relatively inexpensive source of energy to be practical. To give you some idea of the scale of such an operation, the amounts of different energy sources equivalent to the amount of energy needed to melt the iceberg are shown in the table below. Possible sources of the approximately 3.34 × 1011 kJ needed to melt a 1.00 × 106 metric ton iceberg
|
| Exercise 1 |
|---|
| If 17.3 g of powdered aluminum are allowed to react with excess Fe2O3, how much heat is produced? Answer: 273 kJ |
Hess’s Law
Because enthalpy is a state function, the enthalpy change for a reaction depends on only two things: (1) the masses of the reacting substances and (2) the physical states of the reactants and products. It does not depend on the path by which reactants are converted to products. If you climbed a mountain, for example, the altitude change would not depend on whether you climbed the entire way without stopping or you stopped many times to take a break. If you stopped often, the overall change in altitude would be the sum of the changes in altitude for each short stretch climbed. Similarly, when we add two or more balanced chemical equations to obtain a net chemical equation, ΔH for the net reaction is the sum of the ΔH values for the individual reactions. This principle is called Hess’s law, after the Swiss-born Russian chemist Germain Hess (1802–1850), a pioneer in the study of thermochemistry. Hess’s law allows us to calculate ΔH values for reactions that are difficult to carry out directly by adding together the known ΔH values for individual steps that give the overall reaction, even though the overall reaction may not actually occur via those steps.
We can illustrate Hess’s law using the thermite reaction. The overall reaction shown in Equation 9.2.13 can be viewed as occurring in three distinct steps with known ΔH values. As shown in Figure 9.3.1, the first reaction produces 1 mol of solid aluminum oxide (Al2O3) and 2 mol of liquid iron at its melting point of 1758°C (part (a) in Equation 9.3.1); the enthalpy change for this reaction is −732.5 kJ/mol of Fe2O3. The second reaction is the conversion of 2 mol of liquid iron at 1758°C to 2 mol of solid iron at 1758°C (part (b) in Equation 9.3.1); the enthalpy change for this reaction is −13.8 kJ/mol of Fe (−27.6 kJ per 2 mol Fe). In the third reaction, 2 mol of solid iron at 1758°C is converted to 2 mol of solid iron at 25°C (part (c) in Equation 9.3.1); the enthalpy change for this reaction is −45.5 kJ/mol of Fe (−91.0 kJ per 2 mol Fe). As you can see in Figure 9.3.1, the overall reaction is given by the longest arrow (shown on the left), which is the sum of the three shorter arrows (shown on the right). Adding parts (a), (b), and (c) in Equation 9.3.1 gives the overall reaction, shown in part (d):
\( \begin{matrix}
2Al\left ( s, \; 25 ^{o}C \right ) + 2Fe_{2}O_{3}\left ( s, \; 25 ^{o}C \right )& \rightarrow & 2Fe\left ( l, \; 1758 ^{o}C \right ) + 2Al\left ( s, \; 1758 ^{o}C \right ) & \Delta H=-732.5 \; kJ& \left ( a \right ) \\
2Fe\left ( l, \; 1758 ^{o}C \right ) & \rightarrow & 2Fe\left ( s, \; 1758 ^{o}C \right ) & \Delta H=-\;\; 27.6 \; kJ & \left ( b \right )\\
2Fe\left ( s, \; 1758 ^{o}C \right ) + 2Al\left ( s, \; 1758 ^{o}C \right ) & \rightarrow & 2Fe\left ( l, \; 25 ^{o}C \right ) + 2Al\left ( s, \; 25 ^{o}C \right ) & \Delta H=-\;\; 91.0 \; kJ & \left ( c \right )\\
2Al\left ( s, \; 25 ^{o}C \right ) + 2Fe_{2}O_{3}\left ( s, \; 25 ^{o}C \right ) & \rightarrow & 2Al\left ( s, \; 25 ^{o}C \right ) + 2Fe_{2}O_{3}\left ( s, \; 25 ^{o}C \right ) & \Delta H=-852.2 \; kJ & \left ( d \right )
\end{matrix} \tag{9.2.15} \)
The net reaction in part (d) in Equation 9.3.11 is identical to Equation 9.2.13. By Hess’s law, the enthalpy change for part (d) is the sum of the enthalpy changes for parts (a), (b), and (c). In essence, Hess’s law enables us to calculate the enthalpy change for the sum of a series of reactions without having to draw a diagram like that in Figure 9.3.1.
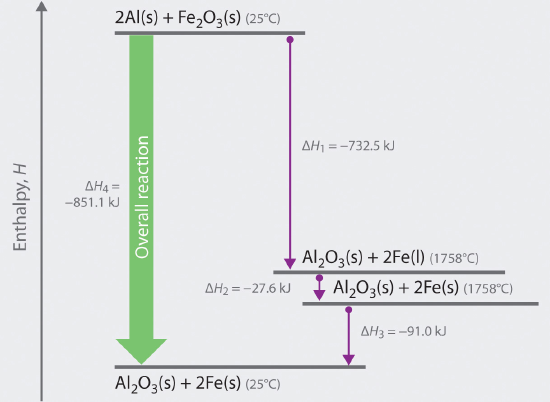
Figure 9.3.1 Energy Changes Accompanying the Thermite Reaction Because enthalpy is a state function, the overall enthalpy change for the reaction of 2 mol of Al(s) with 1 mol of Fe2O3(s) is −851.1 kJ, whether the reaction occurs in a single step (ΔH4, shown on the left) or in three hypothetical steps (shown on the right) that involve the successive formation of solid Al2O3 and liquid iron (ΔH1), solid iron at 1758°C (ΔH2), and solid iron at 25°C (ΔH3). Thus ΔH4 = ΔH1 + ΔH2 + ΔH3, as stated by Hess’s law.
Comparing parts (a) and (d) in Equation 9.3.1 also illustrates an important point: The magnitude of ΔH for a reaction depends on the physical states of the reactants and the products (gas, liquid, solid, or solution). When the product is liquid iron at its melting point (part (a) in Equation 9.3.1), only 732.5 kJ of heat are released to the surroundings compared with 852 kJ when the product is solid iron at 25°C (part (d) in Equation 9.2.15). The difference, 120 kJ, is the amount of energy that is released when 2 mol of liquid iron solidifies and cools to 25°C. It is important to specify the physical state of all reactants and products when writing a thermochemical equation.
When using Hess’s law to calculate the value of ΔH for a reaction, follow this procedure:
- Identify the equation whose ΔH value is unknown and write individual reactions with known ΔH values that, when added together, will give the desired equation.
- Arrange the chemical equations so that the reaction of interest is the sum of the individual reactions.
- If a reaction must be reversed, change the sign of ΔH for that reaction. Additionally, if a reaction must be multiplied by a factor to obtain the correct number of moles of a substance, multiply its ΔH value by that same factor.
- Add together the individual reactions and their corresponding ΔH values to obtain the reaction of interest and the unknown ΔH.
We illustrate how to use this procedure in Example 3.
| Example 3 |
|---|
| When carbon is burned with limited amounts of oxygen gas (O2), carbon monoxide (CO) is the main product: \( \left ( 1 \right ) \;2C\left ( s \right ) + O_{2}\left ( g \right ) \rightarrow 2CO\left ( g \right ) \; \;\ \; \Delta H=-221.0 \; kJ \) When carbon is burned in excess O2, carbon dioxide (CO2) is produced: \( \left ( 2 \right ) \;C\left ( s \right ) + O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( g \right ) \; \;\ \; \Delta H=-393.5 \; kJ \) Use this information to calculate the enthalpy change per mole of CO for the reaction of CO with O2 to give CO2. Given: two balanced chemical equations and their ΔH values Asked for: enthalpy change for a third reaction Strategy: A After balancing the chemical equation for the overall reaction, write two equations whose ΔH values are known and that, when added together, give the equation for the overall reaction. (Reverse the direction of one or more of the equations as necessary, making sure to also reverse the sign of ΔH.) B Multiply the equations by appropriate factors to ensure that they give the desired overall chemical equation when added together. To obtain the enthalpy change per mole of CO, write the resulting equations as a sum, along with the enthalpy change for each. Solution: A We begin by writing the balanced chemical equation for the reaction of interest: \( \left ( 3 \right ) \;CO\left ( g \right ) + \frac{1}{2}O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( g \right ) \; \;\ \; \Delta H_{rxn}=? \) There are at least two ways to solve this problem using Hess’s law and the data provided. The simplest is to write two equations that can be added together to give the desired equation and for which the enthalpy changes are known. Observing that CO, a reactant in Equation 3, is a product in Equation 1, we can reverse Equation (1) to give \( 2CO\left ( g \right ) \rightarrow 2C\left ( s \right ) + O_{2}\left ( g \right ) \; \;\ \; \Delta H=+221.0 \; kJ \) Because we have reversed the direction of the reaction, the sign of ΔH is changed. We can use Equation 2 as written because its product, CO2, is the product we want in Equation 3: \( C\left ( s \right ) + O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( s \right ) \; \;\ \; \Delta H=-393.5 \; kJ \) B Adding these two equations together does not give the desired reaction, however, because the numbers of C(s) on the left and right sides do not cancel. According to our strategy, we can multiply the second equation by 2 to obtain 2 mol of C(s) as the reactant: \( 2C\left ( s \right ) + 2O_{2}\left ( g \right ) \rightarrow 2CO_{2}\left ( s \right ) \; \;\ \; \Delta H=-787.0 \; kJ \) Writing the resulting equations as a sum, along with the enthalpy change for each, gives \( \begin{matrix} Note that the overall chemical equation and the enthalpy change for the reaction are both for the reaction of 2 mol of CO with O2, and the problem asks for the amount per mole of CO. Consequently, we must divide both sides of the final equation and the magnitude of ΔH by 2: \( \begin{matrix} An alternative and equally valid way to solve this problem is to write the two given equations as occurring in steps. Note that we have multiplied the equations by the appropriate factors to allow us to cancel terms: \( \begin{matrix} The sum of reactions A and B is reaction C, which corresponds to the combustion of 2 mol of carbon to give CO2. From Hess’s law, ΔHA + ΔHB = ΔHC, and we are given ΔH for reactions A and C. Substituting the appropriate values gives \( \begin{matrix} This is again the enthalpy change for the conversion of 2 mol of CO to CO2. The enthalpy change for the conversion of 1 mol of CO to CO2 is therefore −566.0 ÷ 2 = −283.0 kJ/mol of CO, which is the same result we obtained earlier. As you can see, there may be more than one correct way to solve a problem. |
| Exercise 3 |
|---|
| The reaction of acetylene (C2H2) with hydrogen (H2) can produce either ethylene (C2H4) or ethane (C2H6): \( \begin{matrix} What is ΔH for the reaction of C2H4 with H2 to form C2H6? Answer: −136.3 kJ/mol of C2H4 |
Enthalpies of Formation and Reaction
One way to report the heat absorbed or released would be to compile a massive set of reference tables that list the enthalpy changes for all possible chemical reactions, which would require an incredible amount of effort. Fortunately, Hess’s law allows us to calculate the enthalpy change for virtually any conceivable chemical reaction using a relatively small set of tabulated data, such as the following:
- Enthalpy of combustion (ΔHcomb): Enthalpy changes have been measured for the combustion of virtually any substance that will burn in oxygen; these values are usually reported as the enthalpy of combustion per mole of substance.
- Enthalpy of fusion (ΔHfus): The enthalpy change that accompanies the melting, or fusion, of 1 mol of a substance; these values have been measured for almost all the elements and for most simple compounds.
- Enthalpy of vaporization (ΔHvap): The enthalpy change that accompanies the vaporization of 1 mol of a substance; these values have also been measured for nearly all the elements and for most volatile compounds.
- Enthalpy of solution (ΔHsoln): The enthalpy change when a specified amount of solute dissolves in a given quantity of solvent.
-
Enthalpy of formation (ΔHf): The enthalpy change for the formation of 1 mol of a compound from its component elements, such as the formation of carbon dioxide from carbon and oxygen. The corresponding relationship is
Equation 5.23
For example,
The sign convention for ΔHf is the same as for any enthalpy change: ΔHf < 0 if heat is released when elements combine to form a compound and ΔHf > 0 if heat is absorbed. The values of ΔHvap and ΔHfus for some common substances are listed in Table 5.1 "Enthalpies of Vaporization and Fusion for Selected Substances at Their Boiling Points and Melting Points". These values are used in enthalpy calculations when any of the substances undergoes a change of physical state during a reaction.
Table 5.1 Enthalpies of Vaporization and Fusion for Selected Substances at Their Boiling Points and Melting Points
| Substance | ΔHvap (kJ/mol) | ΔHfus (kJ/mol) |
|---|---|---|
| argon (Ar) | 6.3 | 1.3 |
| methane (CH4) | 9.2 | 0.84 |
| ethanol (CH3CH2OH) | 39.3 | 7.6 |
| benzene (C6H6) | 31.0 | 10.9 |
| water (H2O) | 40.7 | 6.0 |
| mercury (Hg) | 59.0 | 2.29 |
| iron (Fe) | 340 | 14 |
| Note |
|---|
| The sign convention is the same for all enthalpy changes: negative if heat is released by the system and positive if heat is absorbed by the system. |
Standard Enthalpies of Formation
The magnitude of ΔH for a reaction depends on the physical states of the reactants and the products (gas, liquid, solid, or solution), the pressure of any gases present, and the temperature at which the reaction is carried out. To avoid confusion caused by differences in reaction conditions and ensure uniformity of data, the scientific community has selected a specific set of conditions under which enthalpy changes are measured. These standard conditions serve as a reference point for measuring differences in enthalpy, much as sea level is the reference point for measuring the height of a mountain or for reporting the altitude of an airplane.
The standard conditions for which most thermochemical data are tabulated are a pressure of 1 atmosphere (atm) for all gases and a concentration of 1 M for all species in solution (1 mol/L). In addition, each pure substance must be in its standard state. This is usually its most stable form at a pressure of 1 atm at a specified temperature. We assume a temperature of 25°C (298 K) for all enthalpy changes given in this text, unless otherwise indicated. Enthalpies of formation measured under these conditions are called standard enthalpies of formation (
Figure 5.10 Elemental Carbon

Although graphite and diamond are both forms of elemental carbon, graphite is more stable at 1 atm pressure and 25°C than diamond is. Given enough time, diamond will revert to graphite under these conditions. Hence graphite is the standard state of carbon.
The standard enthalpy of formation of glucose from the elements at 25°C is the enthalpy change for the following reaction:
Equation 5.24
It is not possible to measure the value of
| Example 4 |
|---|
| For the formation of each compound, write a balanced chemical equation corresponding to the standard enthalpy of formation of each compound.
Given: compound Asked for: balanced chemical equation for its formation from elements in standard states Strategy: Use Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" to identify the standard state for each element. Write a chemical equation that describes the formation of the compound from the elements in their standard states and then balance it so that 1 mol of product is made. Solution: To calculate the standard enthalpy of formation of a compound, we must start with the elements in their standard states. The standard state of an element can be identified in Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" by a
|
Exercise 3
For the formation of each compound, write a balanced chemical equation corresponding to the standard enthalpy of formation of each compound.
- NaCl(s)
- H2SO4(l)
- CH3CO2H(l) (acetic acid)
Answer:
Na(s)+12Cl2(g) → NaCl(s) H2(g)+18S8(s)+2O2(g)→H2SO4(l) - 2C(s) + O2(g) + 2H2(g) → CH3CO2H(l)
Standard Enthalpies of Reaction
Tabulated values of standard enthalpies of formation can be used to calculate enthalpy changes for any reaction involving substances whose
) is the enthalpy change that occurs when a reaction is carried out with all reactants and products in their standard states. Consider the general reaction
Equation 5.25
aA + bB → cC + dDwhere A, B, C, and D are chemical substances and a, b, c, and d are their stoichiometric coefficients. The magnitude of
Equation 5.26
More generally, we can write
Equation 5.27
where the symbol Σ means “sum of” and m and n are the stoichiometric coefficients of each of the products and the reactants, respectively. “Products minus reactants” summations such as Equation 5.27 arise from the fact that enthalpy is a state function. Because many other thermochemical quantities are also state functions, “products minus reactants” summations are very common in chemistry; we will encounter many others in subsequent chapters.
| Note |
|---|
| “Products minus reactants” summations are typical of state functions. |
To demonstrate the use of tabulated
Equation 5.28
C6H12O6(s) + 6O2(g) → 6CO2(g) + 6H2O(l)Using Equation 5.27, we write
Equation 5.29
From Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C", the relevant
Equation 5.30
As illustrated in Figure 5.11, we can use Equation 5.29 to calculate
(Recall that when we reverse a reaction, we must also reverse the sign of the accompanying enthalpy change.) The overall enthalpy change for conversion of the reactants (1 mol of glucose and 6 mol of O2) to the elements is therefore +1273.3 kJ.
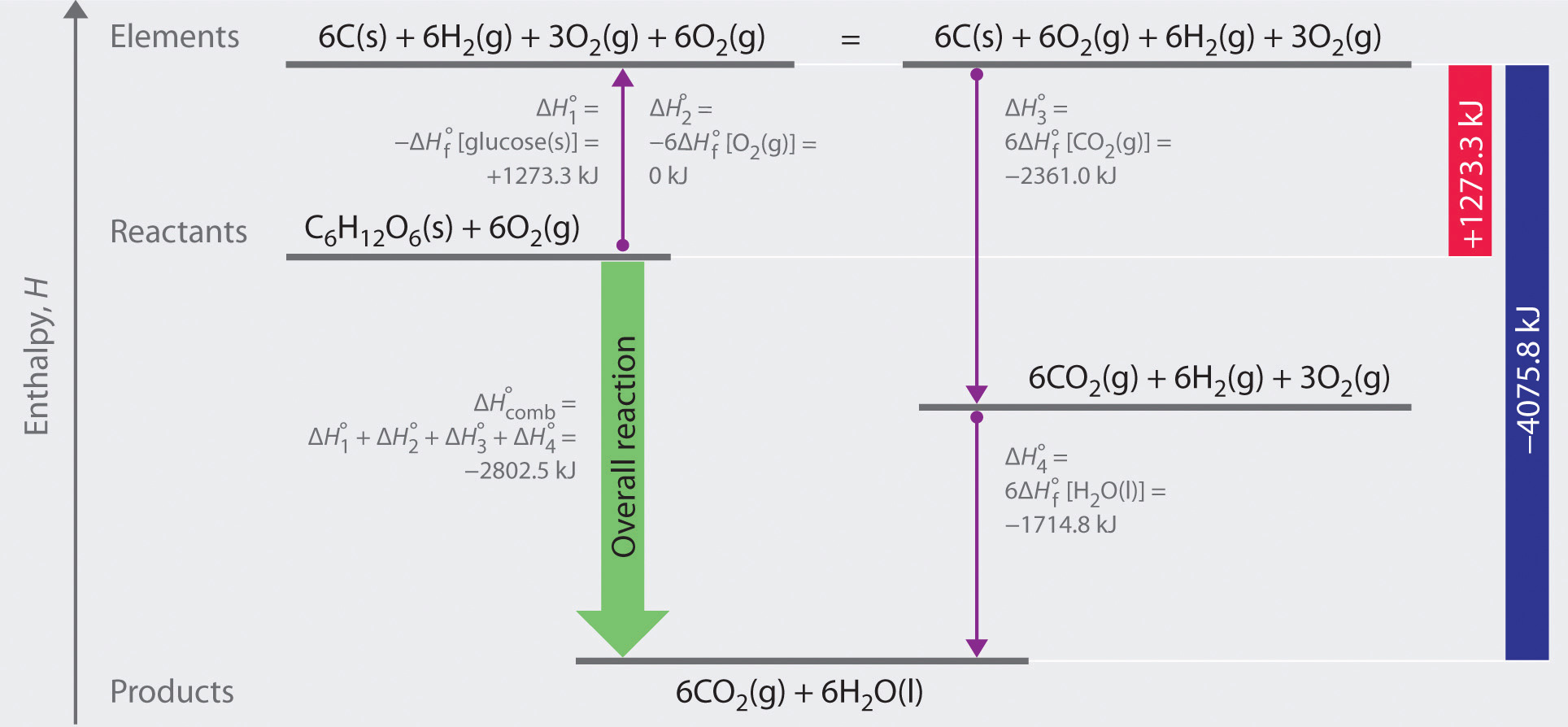
Figure 5.11 A Thermochemical Cycle for the Combustion of Glucose. Two hypothetical pathways are shown from the reactants to the products. The green arrow labeled
The reactions that convert the elements to final products (downward purple arrows in Figure 5.11 "A Thermochemical Cycle for the Combustion of Glucose") are identical to those used to define the
The overall enthalpy change for the conversion of the elements to products (6 mol of carbon dioxide and 6 mol of liquid water) is therefore −4075.8 kJ. Because enthalpy is a state function, the difference in enthalpy between an initial state and a final state can be computed using any pathway that connects the two. Thus the enthalpy change for the combustion of glucose to carbon dioxide and water is the sum of the enthalpy changes for the conversion of glucose and oxygen to the elements (+1273.3 kJ) and for the conversion of the elements to carbon dioxide and water (−4075.8 kJ):
Equation 5.31
This is the same result we obtained using the “products minus reactants” rule (Equation 5.27) and
Example 5
Long-chain fatty acids such as palmitic acid [CH3(CH2)14CO2H] are one of the two major sources of energy in our diet (
Given: compound and
Asked for:
Strategy:
A After writing the balanced chemical equation for the reaction, use Equation 5.27 and the values from Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" to calculate
B Divide this value by the molar mass of palmitic acid to find the energy released from the combustion of 1 g of palmitic acid. Compare this value with the value calculated in Equation 5.30 for the combustion of glucose to determine which is the better fuel.
Solution:
A To determine the energy released by the combustion of palmitic acid, we need to calculate its
Using Equation 5.27 (“products minus reactants”) with
This is the energy released by the combustion of 1 mol of palmitic acid.
B The energy released by the combustion of 1 g of palmitic acid is
As calculated in Equation 5.30,
The combustion of fats such as palmitic acid releases more than twice as much energy per gram as the combustion of sugars such as glucose. This is one reason many people try to minimize the fat content in their diets to lose weight.
Exercise
Use the data in Chapter 25 to calculate
Answer: −41.2 kJ/mol
We can also measure the enthalpy change for another reaction, such as a combustion reaction, and then use it to calculate a compound’s
Example 6
Beginning in 1923, tetraethyllead [(C2H5)4Pb] was used as an antiknock additive in gasoline in the United States. Its use was completely phased out in 1986 because of the health risks associated with chronic lead exposure. Tetraethyllead is a highly poisonous, colorless liquid that burns in air to give an orange flame with a green halo. The combustion products are CO2(g), H2O(l), and red PbO(s). What is the standard enthalpy of formation of tetraethyllead, given that
Given: reactant, products, and
Asked for:
Strategy:
A Write the balanced chemical equation for the combustion of tetraethyllead. Then insert the appropriate quantities into Equation 5.27 to get the equation for
B Convert
C Use Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" to obtain values of
Solution:
A The balanced chemical equation for the combustion reaction is as follows:
2(C2H5)4Pb(l) + 27O2(g) → 2PbO(s) + 16CO2(g) + 20H2O(l)Using Equation 5.27 gives
Solving for
The values of all terms other than
B The magnitude of
Because the balanced chemical equation contains 2 mol of tetraethyllead,
C Inserting the appropriate values into the equation for
Exercise
Ammonium sulfate [(NH4)2SO4] is used as a fire retardant and wood preservative; it is prepared industrially by the highly exothermic reaction of gaseous ammonia with sulfuric acid:
2NH3(g) + H2SO4(aq) → (NH4)2SO4(s)The value of
Answer: −1181 kJ/mol
Enthalpies of Solution and Dilution
Physical changes, such as melting or vaporization, and chemical reactions, in which one substance is converted to another, are accompanied by changes in enthalpy. Two other kinds of changes that are accompanied by changes in enthalpy are the dissolution of solids and the dilution of concentrated solutions.
The dissolution of a solid can be described as follows:
Equation 5.32
solute(s) + solvent(l) → solution(l)The values of ΔHsoln for some common substances are given in Table 5.2 "Enthalpies of Solution at 25°C of Selected Ionic Compounds in Water (in kJ/mol)". The sign and the magnitude of ΔHsoln depend on specific attractive and repulsive interactions between the solute and the solvent; these factors will be discussed in Chapter 13 "Solutions". When substances dissolve, the process can be either exothermic (ΔHsoln < 0) or endothermic (ΔHsoln > 0), as you can see from the data in Table 5.2 "Enthalpies of Solution at 25°C of Selected Ionic Compounds in Water (in kJ/mol)".
Table 5.2 Enthalpies of Solution at 25°C of Selected Ionic Compounds in Water (in kJ/mol)
| Anion | |||||
| Cation | Fluoride | Chloride | Bromide | Iodide | Hydroxide |
| lithium | 4.7 | −37.0 | −48.8 | −63.3 | −23.6 |
| sodium | 0.9 | 3.9 | −0.6 | −7.5 | −44.5 |
| potassium | −17.7 | 17.2 | 19.9 | 20.3 | −57.6 |
| ammonium | −1.2 | 14.8 | 16.8 | 13.7 | — |
| silver | −22.5 | 65.5 | 84.4 | 112.2 | — |
| magnesium | −17.7 | −160.0 | −185.6 | −213.2 | 2.3 |
| calcium | 11.5 | −81.3 | −103.1 | −119.7 | −16.7 |
| Nitrate | Acetate | Carbonate | Sulfate | ||
| lithium | −2.5 | — | −18.2 | −29.8 | |
| sodium | 20.5 | −17.3 | −26.7 | 2.4 | |
| potassium | 34.9 | −15.3 | −30.9 | 23.8 | |
| ammonium | 25.7 | −2.4 | — | 6.6 | |
| silver | 22.6 | — | 22.6 | 17.8 | |
| magnesium | −90.9 | — | −25.3 | −91.2 | |
| calcium | −19.2 | — | −13.1 | −18.0 | |
Substances with large positive or negative enthalpies of solution have commercial applications as instant cold or hot packs. Single-use versions of these products are based on the dissolution of either calcium chloride (CaCl2, ΔHsoln = −81.3 kJ/mol) or ammonium nitrate (NH4NO3, ΔHsoln = +25.7 kJ/mol). Both types consist of a plastic bag that contains about 100 mL of water plus a dry chemical (40 g of CaCl2 or 30 g of NH4NO3) in a separate plastic pouch. When the pack is twisted or struck sharply, the inner plastic bag of water ruptures, and the salt dissolves in the water. If the salt is CaCl2, heat is released to produce a solution with a temperature of about 90°C; hence the product is an “instant hot compress.” If the salt is NH4NO3, heat is absorbed when it dissolves, and the temperature drops to about 0° for an “instant cold pack.”
A similar product based on the precipitation of sodium acetate, not its dissolution, is marketed as a reusable hand warmer (Figure 5.12 "An Instant Hot Pack Based on the Crystallization of Sodium Acetate"). At high temperatures, sodium acetate forms a highly concentrated aqueous solution. With cooling, an unstable supersaturated solution containing excess solute is formed. When the pack is agitated, sodium acetate trihydrate [CH3CO2Na•3H2O] crystallizes, and heat is evolved:
Equation 5.33
A bag of concentrated sodium acetate solution can be carried until heat is needed, at which time vigorous agitation induces crystallization and heat is released. The pack can be reused after it is immersed in hot water until the sodium acetate redissolves.
Figure 5.12 An Instant Hot Pack Based on the Crystallization of Sodium Acetate
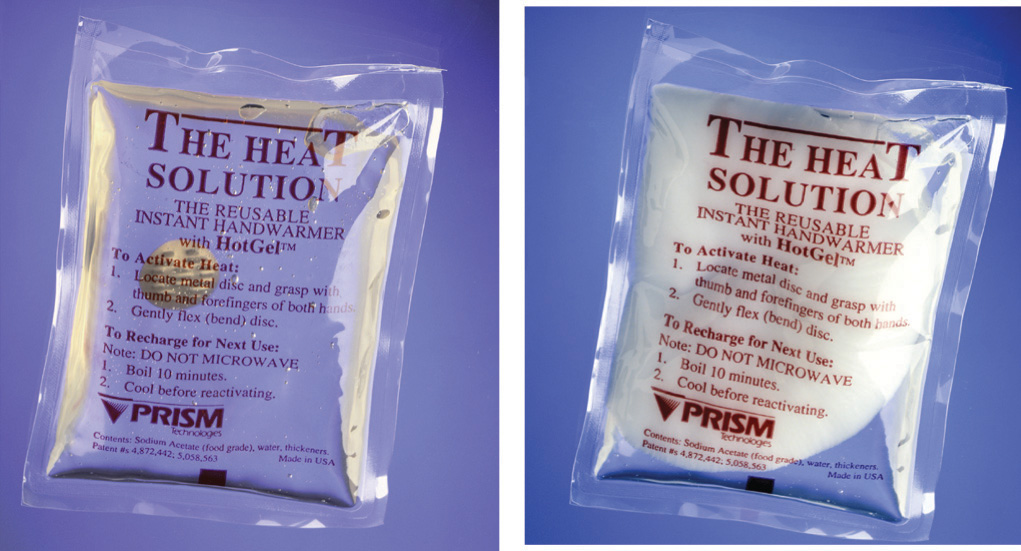
The hot pack is at room temperature prior to agitation (left). Because the sodium acetate is in solution, you can see the metal disc inside the pack. After the hot pack has been agitated, the sodium acetate crystallizes (right) to release heat. Because of the mass of white sodium acetate that has crystallized, the metal disc is no longer visible.
The amount of heat released or absorbed when a substance is dissolved is not a constant; it depends on the final concentration of the solute. The ΔHsoln values given previously and in Table 5.2 "Enthalpies of Solution at 25°C of Selected Ionic Compounds in Water (in kJ/mol)", for example, were obtained by measuring the enthalpy changes at various concentrations and extrapolating the data to infinite dilution.
Because ΔHsoln depends on the concentration of the solute, diluting a solution can produce a change in enthalpy. If the initial dissolution process is exothermic (ΔH < 0), then the dilution process is also exothermic. This phenomenon is particularly relevant for strong acids and bases, which are often sold or stored as concentrated aqueous solutions. If water is added to a concentrated solution of sulfuric acid (which is 98% H2SO4 and 2% H2O) or sodium hydroxide, the heat released by the large negative ΔH can cause the solution to boil. Dangerous spattering of strong acid or base can be avoided if the concentrated acid or base is slowly added to water, so that the heat liberated is largely dissipated by the water. Thus you should never add water to a strong acid or base; a useful way to avoid the danger is to remember: Add water to acid and get blasted!
Key Equations
definition of enthalpy
Equation 5.11: H= E + PV
pressure-volume work
Equation 5.13: w = −PΔV
enthalpy change at constant pressure
Equation 5.14: ΔH = ΔE + PΔV
Equation 5.15: ΔH = qp
relationship between
Equation 5.27:
Summary
In chemistry, the small part of the universe that we are studying is the system, and the rest of the universe is the surroundings. Open systems can exchange both matter and energy with their surroundings, closed systems can exchange energy but not matter with their surroundings, and isolated systems can exchange neither matter nor energy with their surroundings. A state function is a property of a system that depends on only its present state, not its history. A reaction or process in which heat is transferred from a system to its surroundings is exothermic. A reaction or process in which heat is transferred to a system from its surroundings is endothermic.
Enthalpy is a state function used to measure the heat transferred from a system to its surroundings or vice versa at constant pressure. Only the change in enthalpy (ΔH) can be measured. A negative ΔH means that heat flows from a system to its surroundings; a positive ΔH means that heat flows into a system from its surroundings. For a chemical reaction, the enthalpy of reaction (ΔHrxn) is the difference in enthalpy between products and reactants; the units of ΔHrxn are kilojoules per mole. Reversing a chemical reaction reverses the sign of ΔHrxn. The magnitude of ΔHrxn also depends on the physical state of the reactants and the products because processes such as melting solids or vaporizing liquids are also accompanied by enthalpy changes: the enthalpy of fusion (ΔHfus) and the enthalpy of vaporization (ΔHvap), respectively. The overall enthalpy change for a series of reactions is the sum of the enthalpy changes for the individual reactions, which is Hess’s law. The enthalpy of combustion (ΔHcomb) is the enthalpy change that occurs when a substance is burned in excess oxygen. The enthalpy of formation (ΔHf) is the enthalpy change that accompanies the formation of a compound from its elements. Standard enthalpies of formation (
Key Takeaway
- Enthalpy is a state function whose change indicates the amount of heat transferred from a system to its surroundings or vice versa, at constant pressure.
Conceptual Problems
Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 5.6 "Essential Skills 4") before proceeding to the Conceptual Problems.
-
Heat implies the flow of energy from one object to another. Describe the energy flow in an
- exothermic reaction.
- endothermic reaction.
-
Based on the following energy diagram,
- write an equation showing how the value of ΔH2 could be determined if the values of ΔH1 and ΔH3 are known.
- identify each step as being exothermic or endothermic.
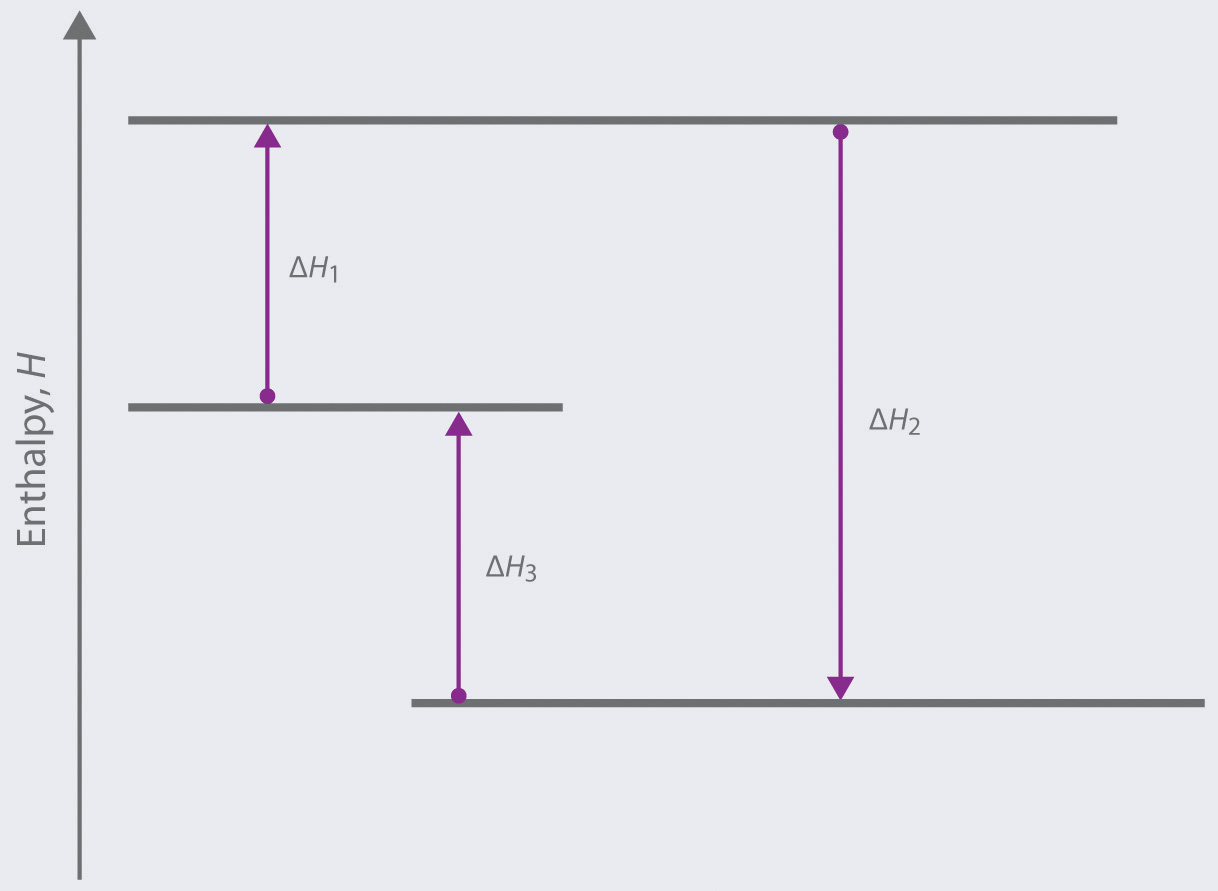
-
Based on the following energy diagram,
- write an equation showing how the value of ΔH3 could be determined if the values of ΔH1 and ΔH2 are known.
- identify each step as being exothermic or endothermic.
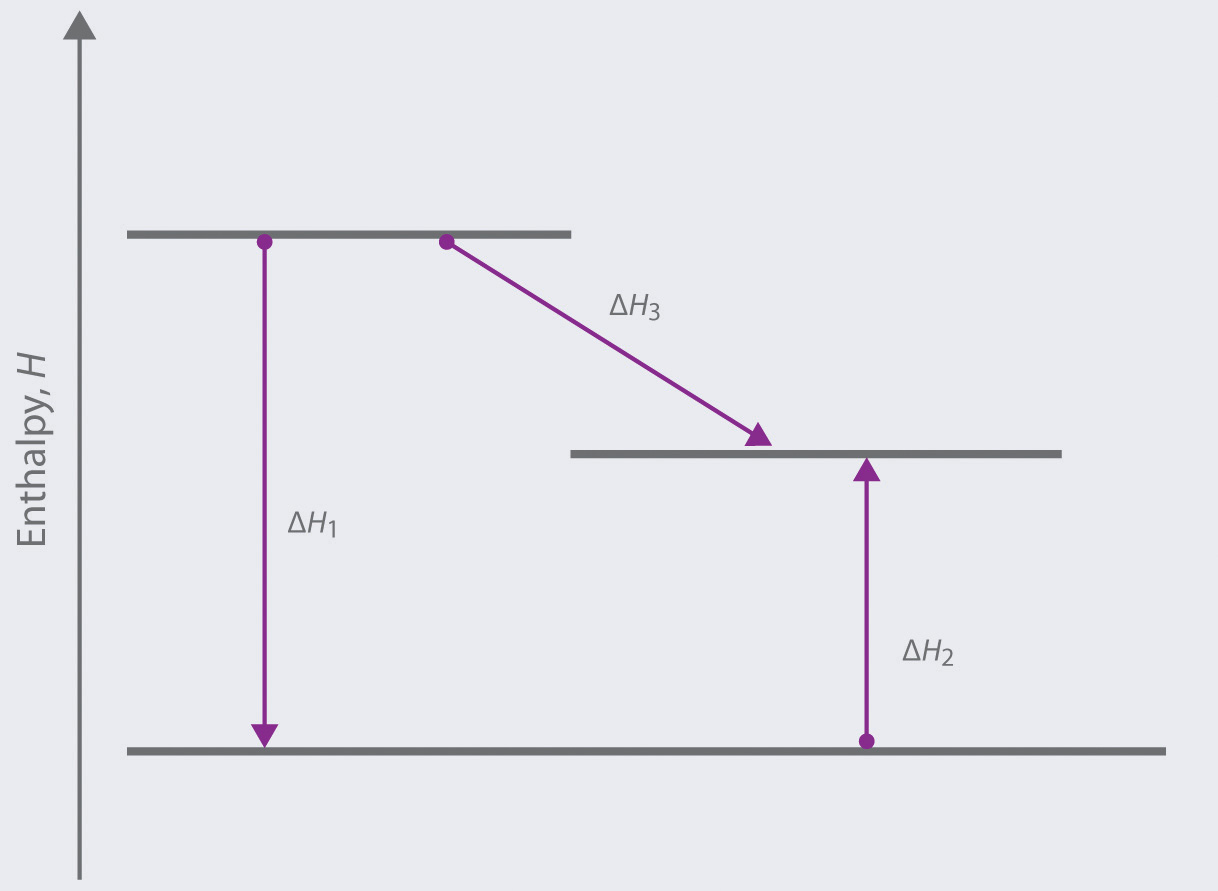
-
When a thermometer is suspended in an insulated thermos that contains a block of ice, the temperature recorded on the thermometer drops. Describe the direction of heat flow.
-
In each scenario, the system is defined as the mixture of chemical substances that undergoes a reaction. State whether each process is endothermic or exothermic.
- Water is added to sodium hydroxide pellets, and the flask becomes hot.
- The body metabolizes glucose, producing carbon dioxide and water.
- Ammonium nitrate crystals are dissolved in water, causing the solution to become cool.
-
In each scenario, the system is defined as the mixture of chemical substances that undergoes a reaction. Determine whether each process is endothermic or exothermic.
- Concentrated acid is added to water in a flask, and the flask becomes warm.
- Water evaporates from your skin, causing you to shiver.
- A container of ammonium nitrate detonates.
-
Is Earth’s environment an isolated system, an open system, or a closed system? Explain your answer.
-
Why is it impossible to measure the absolute magnitude of the enthalpy of an object or a compound?
-
Determine whether energy is consumed or released in each scenario. Explain your reasoning.
- A leaf falls from a tree.
- A motorboat maneuvers against a current.
- A child jumps rope.
- Dynamite detonates.
- A jogger sprints down a hill.
-
The chapter states that enthalpy is an extensive property. Why? Describe a situation that illustrates this fact.
-
The enthalpy of a system is affected by the physical states of the reactants and the products. Explain why.
-
Is the distance a person travels on a trip a state function? Why or why not?
-
Describe how Hess’s law can be used to calculate the enthalpy change of a reaction that cannot be observed directly.
-
When you apply Hess’s law, what enthalpy values do you need to account for each change in physical state?
- the melting of a solid
- the conversion of a gas to a liquid
- the solidification of a liquid
- the dissolution of a solid into water
-
What is the difference between
ΔHοf andΔHf ? -
In their elemental form, A2 and B2 exist as diatomic molecules. Given the following reactions, each with an associated ΔH°, describe how you would calculate
ΔHοf for the compound AB2.2AB→A2+B23AB→AB2+A2B2A2B→2A2+B2ΔHο1ΔHο2ΔHο3 -
How can
ΔHοf of a compound be determined if the compound cannot be prepared by the reactions used to define its standard enthalpy of formation? -
For the formation of each compound, write a balanced chemical equation corresponding to the standard enthalpy of formation of each compound.
- HBr
- CH3OH
- NaHCO3
-
Describe the distinction between ΔHsoln and ΔHf.
-
Does adding water to concentrated acid result in an endothermic or an exothermic process?
-
The following table lists
ΔHοsoln values for some ionic compounds. If 1 mol of each solute is dissolved in 500 mL of water, rank the resulting solutions from warmest to coldest.Compound ΔHοsoln (kJ/mol)KOH −57.61 LiNO3 −2.51 KMnO4 43.56 NaC2H3O2 −17.32
Numerical Problems
Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 5.6 "Essential Skills 4") before proceeding to the Numerical Problems.
-
Using Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C", calculate
ΔHοrxn for each chemical reaction.- 2Mg(s) + O2(g) → 2MgO(s)
- CaCO3(s, calcite) → CaO(s) + CO2(g)
- AgNO3(s) + NaCl(s) → AgCl(s) + NaNO3(s)
-
Using Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C", determine
ΔHοrxn for each chemical reaction.- 2Na(s) + Pb(NO3)2(s) → 2NaNO3(s) + Pb(s)
- Na2CO3(s) + H2SO4(l) → Na2SO4(s) + CO2(g) + H2O(l)
- 2KClO3(s) → 2KCl(s) + 3O2(g)
-
Calculate
ΔHοrxn for each chemical equation. If necessary, balance the chemical equations.- Fe(s) + CuCl2(s) → FeCl2(s) + Cu(s)
- (NH4)2SO4(s) + Ca(OH)2(s) → CaSO4(s) + NH3(g) + H2O(l)
- Pb(s) + PbO2(s) + H2SO4(l) → PbSO4(s) + H2O(l)
-
Calculate
ΔHοrxn for each reaction. If necessary, balance the chemical equations.- 4HBr(g) + O2(g) → 2H2O(l) + 2Br2(l)
- 2KBr(s) + H2SO4(l) → K2SO4(s) + 2HBr(g)
- 4Zn(s) + 9HNO3(l) → 4Zn(NO3)2(s) + NH3(g) + 3H2O(l)
-
Use the data in Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" to calculate
ΔHοf of HNO3(l) ifΔHοrxn=−320.0 kJ for the reaction Sn(s, white) + 4HNO3(l) → SnO2(s) + 4NO2(g) + 2H2O(l). -
Use the data in Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" to calculate
ΔHοf of P4O10(s) ifΔHοrxn=−362.1 kJ for the reaction P4O10(s) + 6H2O(l) → 4H3PO4(l). -
How much heat is released or required in the reaction of 0.50 mol of HBr(g) with 1.0 mol of chlorine gas to produce bromine gas?
-
How much energy is released or consumed if 10.0 g of N2O5 is completely decomposed to produce gaseous nitrogen dioxide and oxygen?
-
In the mid-1700s, a method was devised for preparing chlorine gas from the following reaction:
NaCl(s) + H2SO4(l) + MnO2(s) → Na2SO4(s) + MnCl2(s) + H2O(l) + Cl2(g)Calculate
ΔHοrxn for this reaction. Is the reaction exothermic or endothermic? -
Would you expect heat to be evolved during each reaction?
- solid sodium oxide with gaseous sulfur dioxide to give solid sodium sulfite
- solid aluminum chloride reacting with water to give solid aluminum oxide and hydrogen chloride gas
-
How much heat is released in preparing an aqueous solution containing 6.3 g of calcium chloride, an aqueous solution containing 2.9 g of potassium carbonate, and then when the two solutions are mixed together to produce potassium chloride and calcium carbonate?
-
Methanol is used as a fuel in Indianapolis 500 race cars. Use the following table to determine whether methanol or 2,2,4-trimethylpentane (isooctane) releases more energy per liter during combustion.
Fuel ΔHοcomb (kJ/mol)Density (g/mL) methanol −726.1 0.791 2,2,4-trimethylpentane −5461.4 0.692 -
-
Use the enthalpies of combustion given in the following table to determine which organic compound releases the greatest amount of energy per gram during combustion.
Fuel ΔHοcomb (kJ/mol)methanol −726.1 1-ethyl-2-methylbenzene −5210.2 n-octane −5470.5 - Calculate the standard enthalpy of formation of 1-ethyl-2-methylbenzene.
-
-
Given the enthalpies of combustion, which organic compound is the best fuel per gram?
Fuel ΔHοf (kJ/mol)ethanol −1366.8 benzene −3267.6 cyclooctane −5434.7
Answers
-
- −1203 kJ/mol O2
- 179.2 kJ
- −59.3 kJ
-
-
-
-
−174.1 kJ/mol
-
-
−20.3 kJ
-
-
−34.3 kJ/mol Cl2; exothermic
-
-
ΔH = −2.86 kJ CaCl2: −4.6 kJ; K2CO3, −0.65 kJ; mixing, −0.28 kJ
-
-
-
To one decimal place
methanol: ΔH/g = −22.6 kJ C9H12: ΔH/g = −43.3 kJ octane: ΔH/g = −47.9 kJOctane provides the largest amount of heat per gram upon combustion.
-
ΔHf(C9H17) = −46.1 kJ/mol
-

